解:1000-1=999
997-995=992
每次减少7,999/7=12……5
所以下面减上面最小是5
1333-1=1332 1332/7=190……2
所以上面减下面最小是2
因此这个差最小是2。
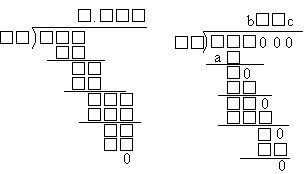
2. 如果四位数6□□8能被73整除,那么商是多少?
解:估计这个商的十位应该是8,看个位可以知道是6
因此这个商是86。
3. 求各位数字都是 7,并能被63整除的最小自然数。
解:63=7*9
所以至少要9个7才行(因为各位数字之和必须是9的倍数)
4. 1×2×3×…×15能否被 9009整除?
解:能。
将9009分解质因数
9009=3*3*7*11*13

5. 能否用1, 2, 3, , 5, 6六个数码组成一个没有重复数字,且能被11整除的六位数?为什么?
解:不能。因为1+2+3++5+6=21,如果能组成被11整除的六位数,那么奇数位的数字和与偶数位的数字和一个为16,一个为5,而最小的三个数字之和1+2+3=6>5,所以不可能组成。
6. 有一个自然数,它的最小的两个约数之和是,最大的两个约数之和是100,求这个自然数。
解:最小的两个约数是1和3,最大的两个约数一个是这个自然数本身,另一个是这个自然数除以3的商。最大的约数与第二大
7.100以内约数个数最多的自然数有五个,它们分别是几?
解:如果恰有一个质因数,那么约数最多的是=64,有7个约数;
如果恰有两个不同质因数,那么约数最多的是×=72和×3=96,各有12个约数;
如果恰有三个不同质因数,那么约数最多的是×3×5=60,×3×7=84和2××5=90,各有12个约数。
所以100以内约数最多的自然数是60,72,84,90和96。
8. 写出三个小于20的自然数,使它们的最大公约数是1,但两两均不互质。
解:6,10,15
9. 有336个苹果、 252个桔子、 210个梨,用这些果品最多可分成多少份同样的礼物?在每份礼物中,三样水果各多少?
解:2份;每份有苹果8个,桔子6个,梨5个。
10. 三个连续自然数的最小公倍数是168,求这三个数。
解:6,7,8。提示:相邻两个自然数必互质,其最小公倍数就等于这两个数的乘积。而相邻三个自然数,若其中只有一个偶数,则其最小公倍数等于这三个数的乘积;若其中有两个偶数,则其最小公倍数等于这三个数乘积的一半。
 爱华网
爱华网