摘 要:算法是《普通高中数学课程标准》中新增加的内容,算法在高考中重点考查算法的概念和算法的三种逻辑结构。以选择题或填空题的形式出现,考察的热点是算法的含义、流程图、基本算法语句等内容。同时在高考中算法初步知识与函数、数列、三角、概率、实际问题等知识点进行整合,是高考试题命制的新趋势,该类问题具有一定的综合性,可以考查学生的识图能力及对数列知识的掌握情况,因此在高中算法教学中应该引起足够的重视。
关键字:算法;算法的基本语句;算法教学
Research entrance "algorithm preliminary" thinking high school teaching algorithms
Abstract: The algorithm is "high school math curriculum standards," the new additions, the algorithm in the entrance focus on examining the concept of algorithm and algorithm of the three logical structure. Multiple-choice or fill-in form, examining the meaning of hot spots is algorithm, flow chart, the basic algorithm statement and so on. Algorithm in the entrance while the initial knowledge and functions, series, trigonometry, probability, knowledge of practical problems such as integration points, is the College Entrance Examination system of the new trend of life, the problem with a certain type of comprehensive, you can examine the student's ability and knowledge map the number of columns of mastery of knowledge, so the algorithm in high school teaching should arouse enough attention.
Keywords: Algorithm; algorithm basic statements; algorithm teaching
算法是《普通高中数学课程标准》中新增加的内容,在教学中应该处理该部分内容呢?下面本人将从新课标和新高考角度来谈谈高中阶段算法的教学。
一、高考考查的形式与特点
算法初步是高中新课标增加的内容,与前面的知识有着密切的联系,并且与实际问题的联系也非常密切。算法不仅是数学及其应用的重要组成部分,也是计算机科学的重要基础。因此,在高考中算法初步知识将与函数、数列、三角、概率、实际问题等知识点进行整合,是高考试题命制的新趋势。这样试题就遵循了“在知识网络交汇处设计试题”的命制原则,既符合高考命题“能力立意”的宗旨,又突出了数学的学科特点。这样做,可以从学科的整体高度和思维价值的高度考虑问题,可以揭示数学各知识之间得到的内在联系,可以使考查达到必要的深度。
归结新高考试题特点,可以发现算法考查形式与特点是:
(1) 选择题、填空题主要考查算法的含义、流程图、基本算法语句等内容,一般在每份试卷中有1~2题,多为中档题出现。
(2) 在解答题中可通过让学生读程序框图去解决其它问题,此类试题往往是与数列题结合在一起,具有一定的综合性,可以考查学生的识图能力及对数列知识的掌握情况。
二、高考命题趋向与预测
1.考查算法的基本语句
这类题型主要考查对基本算法语句的理解和应用,高考对算法语句的考查一般以选择题、填空题的形式考查,一是对一个算法程序中缺少的关键语句进行补充,二是写出一个算法执行后的结果,难度不会太大。解答这类题目应注意熟练掌握赋值语句、条件语句、循环语句的格式,能够根据题目的要求,利用恰当的算法语句设计算法。
例1:“x=3*5”,“x=x+1”是某一程序中的先后相邻的两个语句,那么下列说法中正确的是( )
① x=3*5的意思是x=3*5=15,此式与算术中的式子是一样的;
② x=3*5是将数值15赋给x;
③ x=3*5可以写成3*5=x;
④ x=x+1语句执行时,“=”右边x的值是15,执行后左边x的值是16。
A.①③ B.②④ C.①④ D.②③
解析:由赋值语句的特点本题应选B。
点评:本题主要考查赋值语句,在赋值语句中变量必须在等号的左边,表达式必须在等号的右边;一个语句只能给一个变量赋值,将一个变量的赋值给另一个变量,前一个变量的值保持不变;可先后给一个变量赋多个不同的值,但变量的取值总是最近被赋予的值。
例2:给出以下算法:
S1 i=3,S=0
S2 i=i+2
S3 S=S+i
S4 S≥2009?如果S≥2009,执行S5;否则执行S2
S5 输出i
S6 结束
则算法完成后,输出的i的值等于 。
解析:根据算法可知,i的值in构成一个等差数列{in},S的值是数列{in}相应的前n项的和,且i1=5,d=2,所以in=2n+1。又S≥2009,所以n≥43,故in=89,所以输出的i的值为89。
点评:本题主要结合数列的知识考查用自然语言描述的算法,解题的关键是要理解S4。
2.考查程序框图的功能
此类题目有两种题型:一是给出程序框图来指出功能;二是指出程序框图输出的结果。可以考查学生阅读算法程序框图的能力,对算法理解的程度,这是算法初步试题的重要题型之一。
例1、如图,下列程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数)。如果输入1000,输出的结果为788,则运用此方法估计的π的近似值为 (保留四位有效数字)。
解析:本题转化为用几何概型求概率的问题。根据程序框图知,如果点在圆x2+y2=1内,m就相加一次;现N输入1000,m起始值为0。输出结果为788,说明m相加了788次,也就是说有788个点在圆x2+y2=1内。设圆的面积为S1,正方形的面积为S2,则概率P==
∴π=4p=4×≈3.152
点评:本题是算法框图与几何概型的整合,融合自然,具有创新性,有力地考查了基础知识和逻辑思维能力,同时又能体会到求无理数近似值的一种算法,可培养学生用数学的意识。
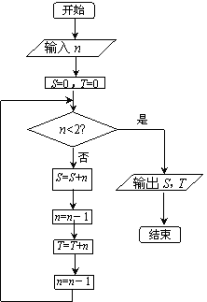
例2 (2007 高考山东)阅读右边的程序框图,若输入的n是100,则输出的变量S和T的值依次是( )
A.2500,2500 B.2550,2550
C.2500,2550 D.2550,2500
解析:由程序框图知,S=100+98+96+……+2=2550
T=99+97+95+……+1=2500,选D
点评:该题主要考查算法流程图、等差数列求和等基础知识,以及算法思想、数据处理能力、语言转换能力。本题采用直到型循环语句描述算法,解题的关键是循环体中两个n=n-1的理解,明确循环一次后n的值就减少了2。
3.完善程序框图中的条件或内容
在不完整的程序框图中,填补一些条件或内容,是高考考查算法知识的一种重要题型,应引起足够的重视。此类试题要求学生要有比较扎实的算法初步的基本知识,以及综合分析问题和解决问题的能力,对学生要求较高。
【例1】 一个算法的程序框图如右图所示,若该程序输出的结果为,则判断框中应填入的条件是 。
解析:由循环体可知,当sum=1时,s=0+;当sum=2时,s=+=,……,当sum=4时,s=+=,因此,判断框中应填:“i<5?”或“sum<4?”
点评:本题设计角度比较新颖,具有探索性,同时答案又具开放性。此题融算法、数列求和于一体,虽属常规题,但由于问法不同,有力考查学生对数列、框图等知识的掌握情况以及分析问题和解决问题的能力。
【例2】 (07高考广东)如图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1、A2、……、A10(如A2表示身高(单位:cm)在[150,155)内的学生人数)。
图2是统计图1中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
A.i<6 B.i<7 C.i<8 D.i<9
解析:这题实质是一个当型循环结构设计的算法,由题意要统计身高在160~180cm(含160cm,不含180cm)的学生人数,事实上,是图1中条形图从第四个矩形到第七个矩形所对应的人数之和,即A4+A5+A6+A7,因此由循环结构,在流程图中的判断结构内应填写的条件应是i<8,故选C。
点评:本题主要考查程序框图中的当型循环结构及统计学中的知识,体现出在知识网络的交汇处命题的原则。解题的关键是了解条形图的统计知识和当型循环结构的特点,并注意WHILE型语句与UNTIL型语句之间的区别。
4.设计流程图或编写程序解决问题
设计流程图或编(改)写程序解决问题,是算法初步试题中要求比较高难度也比较大的一种题型,此类试题一般会在解答题中出现,以算法为载体,同时也可与其它主干知识点进行交汇,要求学生对算法要有本质的理解,这样命题不仅关注学生的思维结果,更关注学生的思维过程。
【例3】 根据下面的要求,求满足1+2+3+4+……+n>560的最小自然数n。
(1) 要求画出执行该问题的程序框图;
(2) 以下是解决该问题的一个程序,但有几处错误,请找出错误并在右边改正。
i=1
s=1
n=0
Do s<=560
s=s+i
i=i+1
n=n+1
WEND
PRINT n+1
END
解析:(1)程序框图如下图所示:
(2)应将“s=1”改为“s=0”;“Do”改为“WHILE”;“PRINT n+1”改为“PRINT n”
点评:本题主要是结合不等式考查程序框图的理解和应用能力,具有创新性。解决本题的关键是要对循环次数的理解,以及循环语句中“当型”和“直到型”的区别。在画循环结构的程序框图时应注意选择合理的循环变量及判断框内的条件。
5.解决实际问题
在编程的过程中,常常遇到实际问题,增加了解题的难度,处理这类问题的基本思路是:分析实际问题──建立数学模型──设计程序框图──用算法语言描述。此类试题情境设置比较新颖,可以考查学生的应用意识,使学生领悟算法思想不但体现在计算机程序设计中,还体现在日常生活中。
铁路托运行李,从甲地到乙地,按规定每张客票托运行李不超过50kg时,每千克0.2元,超过50kg时,超过部分按每千克0.25元计算,某同学画出了计算行李价格的算法框图(如图所示),则在程序框图中(1)应填的内容是 ;(2)应填的内容是 。
解析:由题意这两处分别应填y=0.2*50+0.25*(x-50)和y=0.2*x。
点评:本题主要考查关于条件语句的应用问题。通过数学建模,将实际问题转化为分段函数问题,关于分段函数的题目在设计程序时都会用到条件语句,分类的标准是条件语句的条件。
6.算法初步知识的综合应用
算法初步的综合应用主要体现在算法框图与数列的综合题联系在一起,此类试题综合性强、灵活性大,保持了能力立意的特点,备受命题者的青睐,成为新课标高考的一大亮点,是高考试题命制的全新尝试。
【例4】 根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,……,xn,……,x2008;y1,y2,……,yn,……,y2008。
(1) 求数列{xn}的通项公式xn;
(2) 写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论;
(3) 求zn=x1y1+x2y2+……+xnyn(x∈N*,n≤2008)
解析:(1)由题意和框图知,数列{xn}中,x1=1,xn+1=xn+2
∴xn=1+2(n-1)=2n-1(n∈N*,n≤2008)
(2)y1=2,y2=8,y3=26,y4=80
由此猜想yn=3n-1(n∈N*,n≤2008)
证明:由框图知,数列{yn}中,yn+1=3yn+2
∴yn+1+1=3(yn+1)
∴=3,y1+1=3
∴数列{yn+1}是以首项为3,公比为3的等比数列。
∴yn+1=3·3n-1=3n
∴yn=3n-1(n∈N*,n≤2008)
(3)zn= x1y1+x2y2+……+xnyn
=1×(3-1)+3×(32-1)+……+(2n-1)·(3n-1)
=1×3+3×32+……+(2n-1)·3n-[1+3+……+(2n-1)]
记Sn=1×3+3×32+……+(2n-1)·3n ①
则3Sn= 1×32+3×33+……+(2n-1)·3n+1 ②
①-②得-2Sn=3+2×32+2×33+……+2×3n-(2n-1)·3n+1
=2(3+32+……+3n)-3-(2n-1)·3n+1
=2×-3-(2n-1)·3n+1=2(1-n)·3n+1-6
∴Sn=(n-1)·3n+1+3
而1+3+……+(2n-1)=n2
∴zn=(n-1)·3n+1+3-n2(n∈N*,n≤2008)
点评:本题主要考查学生对流程图的识别能力以及数列中的归纳、猜想、论证等能力,同时考查通过构造数列求通项公式、错位相减法求和等重点方法。试题体现了以能力立意、一般能力、研究型问题的特点和要求,同时在算法的考查中对流程图的阅读理解能力的要求越来越高。
三、算法教学的思考
算法虽然是高中数学课程第一次引入的内容,需要一个熟悉的过程,但实际上算法的思想大家并不陌生,只是过去没有明确提“算法”一词而已。然而,我们在高三复习时不够重视,往往都是这部分内容放到最后,复习时基本上做两套试卷就算过去,学生对这部分的学习多是机械的,难以从本质上加以理解,导致学生对此内容掌握不到位,解决问题能力较差。因此,在高教学中,必须重视对算法初步的深入学习。
1) 突出重点,突破难点,体会算法思想
在算法的学习中,首先应当克服畏难情绪,应从课本上的典型实例及历年高考所考算法部分的题目着手,分析其中蕴含的算法思想,体会算法“通用化”、“机械化”、“程序化”的特点以及对算法步骤“明确”、“有效”、“有限”的要求。其次,以具体算法案例为载体,通过分析和阐明算理、明确算法步骤、用程序框图表示、将程序框图翻译成计算机语言(写程序语句)等体会算法思想;利用“思考”、“探究”等栏目,思考和探究算法的特点,认识程序框图的三种基本逻辑结构等;通过比较同一个问题的不同算法中的算理,体会好算法的特点,并学会改进算法;鼓励算法的多样性,鼓励通过讨论和交流丰富学生对算法的认识,提高算法设计的能力。
2) 重视基础知识的理解和掌握
学习算法首先要掌握算法概念和算法的基本思想,注意算法与一般意义上具体问题的解法的联系与区别。其次,了解算法的含义,了解算法的思想、理解程序框图的三种基本逻辑结构:顺序结构、条件分支结构、循环结构;理解几种基本算法语句--输入语句、输出语句、赋值语句、条件语句、循环语句的含义。另外,在算法复习时要注意将算法与其它数学内容联系,也要关注将算法思想渗透到后续的高中数学课程的学习中去,尽可能地运用算法解决相关问题。
3) 把握基本题型、基本思想
算法初步的题型主要有:
(1)在了解算法含义和算法思想的基础上,考查算法的一些简单的设计问题,并能够正确地分析和理解一个给定的算法;
(2)考查学生熟练地写出已有程序的运行结果,能够画出各种程序框图并编写程序或完善程序框图中的条件或内容;
(3)解决综合问题。
高考对算法的考查,一个显著的特点便是高度的综合,算法可以与函数、数列、三角、概率等知识整合在一起组合成综合题,加强对算法初步的复习显得尤其重要。
4) 算法复习应尽量使用信息技术
算法复习中,应当鼓励学生尽可能上机尝试。上机能极大地提高学生学习算法的兴趣:不但可以检验算法的正确性以及算法的好坏,而且还可以通过改进算法而引起学生对算法的更深入思考。例如,在“质数判定”的算法中,可以引导学生思考改进算法的方法,把“检验2,3,……,(n-1)是不是n的因数”改为“检验2,3,……,(其实是的整数部分)是不是n的因数”,从而大大地提高运算速度,使学生体会数学知识在优化算法中的重要作用。
2011-09-27 人教网 爱华网
爱华网