3.1 卡诺图简介(2)
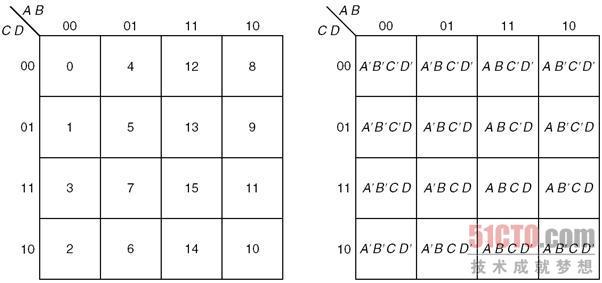
卡诺图3.7 含列标注的卡诺图
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=206 alt="" src="http://pic.aIhUaU.com/201602/15/110102448.jpg" width=273 border=0>[/TD][/TR]
[TR][/TR]
四变量卡诺图有16个小方块,是按照4×4形式排列的,如卡诺图3.8所示。
同三变量卡诺图一样,相邻方块中的1(最上最下行以及最左最右列也认为是相邻的)对应一个乘积项(使用P9a进行合并)。示例3.2中给出3个这种乘积项。
卡诺图3.8 四变量卡诺图
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=283 alt="" src="http://pic.aIhUaU.com/201602/15/110134484.jpg" width=602 border=0>[/TD][/TR]示例3.2
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=313 alt="" src="http://pic.aIhUaU.com/201602/15/110154988.jpg" width=643 border=0>[/TD][/TR]
到目前为止,我们给出的所有乘积项都是使用P9a将两个最小项合并后得到的对应乘积项。这些乘积项仅消去了一个字母,即在三变量函数中得到的是两字母乘积项,四变量函数中得到的是三字母乘积项。下面我们来看卡诺图3.9中给出的4个1为一组的卡诺图。
在左边的卡诺图中,我们圈出两组,一组对应的乘积项为 ,另一组对应的乘积项为AC。显然,在得到的两个乘积项上能使用P9a,得到
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=22 alt="" src="http://pic.aIhUaU.com/201602/15/110227546.jpg" width=110 border=0>[/TD][/TR]卡诺图3.9 4个1为一组的卡诺图
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=161 alt="" src="http://pic.aIhUaU.com/201602/15/110246741.jpg" width=459 border=0>[/TD][/TR]
如右边的卡诺图所示,这是4个1组成的一个矩形。通常情况下,由4个1组成的矩形对应的乘积项会消去两个字母(即在三变量函数中得到的是一字母乘积项,四变量函数中得到的是两字母乘积项)。
可从这些最小项中提取公因子 ,得到
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=31 alt="" src="http://pic.aIhUaU.com/201602/15/110330458.jpg" width=501 border=0>[/TD][/TR]可以看到,括号中的和就是变量 、 的所有最小项的和,结果肯定为1。因此,只需一步就能得到最终的结果。实际上,可以对P9增加一条补充性质,为
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=57 alt="" src="http://pic.aIhUaU.com/201602/15/110350669.jpg" width=515 border=0>[/TD][/TR]该补充性质的证明只需反复使用P9即可。首先对前两项使用P9,然后对后两项使用P9,最后再对前面两次得到的结果使用P9,具体过程如下:
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=60 alt="" src="http://pic.aIhUaU.com/201602/15/110408606.jpg" width=423 border=0>[/TD][/TR]
卡诺图3.10中给出了四变量问题中含4个1为一组的情况的示例。
卡诺图3.10 4个1为一组的情况示例
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=217 alt="" src="http://pic.aIhUaU.com/201602/15/110434600.jpg" width=643 border=0>[/TD][/TR]
根据图确定所对应乘积项的最简单的方法就是通过确定所有1在图中所在的行和列。因此,在第一张图中,由于左边的一组1全位于00( [I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=22 alt="" src="http://pic.aIhUaU.com/201602/15/110859893.jpg" width=29 border=0> )列,因此其对应的乘积项为[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=22 alt="" src="http://pic.aIhUaU.com/201602/15/110859893.jpg" width=29 border=0>。另外一组的1位于11和10列,这两列的公因子是A(对应A);此外组中的1是位于01和11两行,这两行的公因子是D。因此,该组1对应的乘积项为AD。中间这张图中,1是在00和10列中,得到[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=20 alt="" src="http://pic.aIhUaU.com/201602/15/110837618.jpg" width=21 border=0> ;且在01和11行中,得到D,因此其对应的乘积项为[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=25 alt="" src="http://pic.aIhUaU.com/201602/15/110800960.jpg" width=36 border=0>。(顺便说一下,该项也在第一张图中出现,只是我们未将其圈为一组。)最后一张图中,四个角对应的乘积项为[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=25 alt="" src="http://pic.aIhUaU.com/201602/15/110800960.jpg" width=36 border=0> (由于所有的1位于00或10列以及00或10行)。中间一组对应的乘积项为BD。当然,我们通过代数法也能得到这些乘积项,首先写出最小项,然后成对使用P10a,再对得到的乘积项使用P10a(如在三变量示例中的化简过程所做)。然而使用卡诺图可省去我们做代数运算。
两个四个一组的相邻项可用类似的方法组成一个8个方块一组的形式(可消去3个字母)。卡诺图3.11中给出了两个这样的组的示例。左侧的图对应的项是[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=26 alt="" src="http://pic.aIhUaU.com/201602/15/110730930.jpg" width=21 border=0> ,右侧的图对应的项是[I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=23 alt="" src="http://pic.aIhUaU.com/201602/15/110707565.jpg" width=19 border=0> 。
卡诺图3.11 8个1一组的卡诺图
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=233 alt="" src="http://pic.aIhUaU.com/201602/15/110639863.jpg" width=512 border=0>[/TD][/TR]我们可以将所有的函数用卡诺图表示。若已经知道函数中所含的最小项,可直接利用它们填写卡诺图,或者可以将函数写成SOP形式,按每个乘积项对应的卡诺图中的位置进行填写。
 爱华网
爱华网