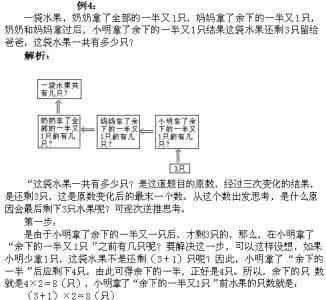
28.计算比较
例如,九册思考题:1÷11、2÷11、3÷11……10÷11。想一想,得数有什么规律?
……
可见,除数是11,被除数是1的几倍(倍数不得大于或等于11),商
17÷11=(11+6)÷11=11÷11+6÷11
凡商是纯循环小数的除式,都有此规律;不是纯循环小数的,得数不存在这一规律。
不难发现,它们循环节的位数比除数少1,循环数字和顺序相同,只是起点不同。
只要记住1÷7的循环节数字“142857”和顺序,计算时以最大商的数字为起点,顺序写出全部循环节数字,即可。
29.由验算想
例如,思考题:计算1212÷101,……,3939÷303,你能从计算中得到启发,很快说出下面各题的得数?
4848÷202,7575÷505,……
3939÷303
=(3030+909)÷303
=3030÷303+909÷303
=10+3=13
备课用书这种由“除法的分配律”解,要使三年级学生接受,比较困难。
若从“除法的验算”推导
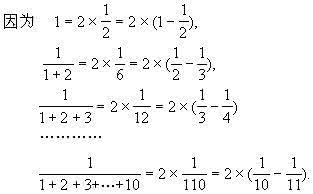
由3939÷303=( ),
商百位上的3和13相乘才可得39,商个位上的3也必须与13相乘得39,除数是13确定无疑。显然,在被除数上面写上除数,使位数对齐,口算很快会得出结果。
所以商是12。
30.想 倍 比
31.扩 缩 法
例如,两数和是42,如果其中一个数扩大5倍,另一个数扩大4倍,则和是181。求这两个数。
若把和,即这两个数都扩大4倍,则得数比181小,因为原来扩大5倍的那个数少扩大了1倍。差就是那个数。
181-42×4=13
42-13=29
若把两数都扩大5倍,结果比181多了原来扩大4倍的那个数。
42×5-181=29,42—29=13。
若把181缩小4倍,则得数比42大。因为其中的一个数先扩大5倍,又
若把181缩小5倍,得数比42小。因为先扩大4倍的那个数,又缩小5
最佳想法:
两数扩大的倍数不同,181不会是42的整倍数。相除就把多扩大1倍的那个数以余数形式分离出来。
181÷42=4余13。
另个数可这样求
32.分别假设
例如,1992年中学数学奥林匹克试题初赛(C)卷题5:把一个正方形的一边减少20%,另一边增加2米,得到一个长方形,它与原来的正方形面积相等。那么,正方形的面积是多少平方米。
设正方形的边长为1,另一边增加的百分数为x,则
(1-1×20%)×(1+x)=1,
正方形边长 2÷25%=8(米),
面积 8×8=64(平方米)。
 爱华网
爱华网