gong'e quxian
共轭曲线
conjugate curves
两构件上用以实现给定运动规律的连续相切的一对曲线。曲线与尖点接触可看作为共轭曲线的特例。齿轮传动中一个齿轮推动另一个齿轮转动和凸轮机构中凸轮推动从动件按要求的规律运动,都是依靠共轭曲线来完成的。单就齿轮传动来说,通过做成齿廓的一对对共轭曲线可以得到满足要求传动比的转动(如圆柱齿轮传动),或进行转动与移动间的运动转换(如齿轮与齿条传动),也可获得变速运动(如非圆齿轮传动)等。
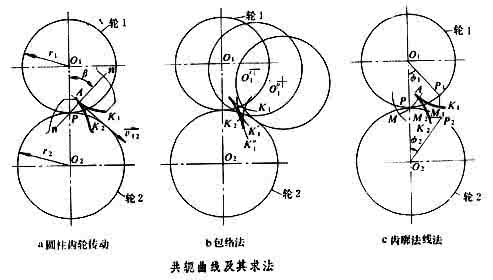
作为平面运动的一对共轭曲线与一对瞬心线(见瞬心)相同之处都是点接触,但瞬心线之间是纯滚动,而共轭曲线在接触点处存在滑动。以共轭曲线作为构件廓线的共轭曲线机构,在传递运动的同时也一定存在有同样运动规律的一对瞬心线。例如一对等速比传动的圆柱齿轮,其瞬心线为相互滚动的一对节圆(见图[共轭曲线及其求法])。
一对共轭曲线在相对运动过程中互为包络线。作为共轭曲线的基本条件,亦即保证两曲线在啮合过程连续相切的条件,是共轭曲线接触点A处的相对速度[vc]12与通过该点所作这对共轭曲线的公法线-垂直,如果这对共轭曲线是一对齿廓曲线,这个性质也称作齿廓啮合基本定律。公法线与两轮中心连线的交点P为两轮的瞬心,也称为节点。
给出两构件的运动要求和共轭曲线中的一条曲线,就可求出另一条曲线,常用的有包络法和齿廓法线法。
包络法 根据一对共轭曲线在相对运动过程互为包络线的原理,如果给定其中一条曲线K1及两轮相对滚动的一对瞬心线(如图[共轭曲线及其求法]中的两节圆)使轮1对轮2作相对运动,即令轮2固定,节圆1在节圆 2上滚动,可得到K1在轮2上的一系列相对位置K1、K、K、…。这些曲线形成一个曲线族。作这个曲线族的包络线K2,即使K2与曲线族中的每条曲线都相切,K2与K1即为一对共轭曲线。K2不仅可用图解法求得,也可采用解析法。解析法首先是在轮1和轮2上分别加上两个动标,在动标1上写出曲线K1的方程(1,1)=0,给出两轮的转角关系[o1]2=[o1]2([o1]1),然后用坐标转换的方法求得K1在动标 2上的曲线族方程(2,2,[o1]1)=0,则包络线方程即为
(2,2,[o1]1)=0
[242-2]
齿廓法线法 这种方法比包络法方便些。其实质是满足齿廓啮合基本定律的运动法,即过共轭曲线接触点的公法线必须通过节点 P。齿廓法线法也可用图解法或解析法。用图解法求解时,在已知曲线K1上任取一点1,过1作K1的法线1P1交节圆 1于P1点。由于P1不是节点,因此1不是接触点。但将轮1转过[o1]1角后,法线1P1转到P位置,显然点就是K1上1点的接触位置。由于两节圆存在滚动的关系,在轮1转[o1]1角的同时轮2转[o1]2角,因此可找到与1对应的K2上的2点。这两点都转到点位置接触。用这种方法在齿廓1上给出一系列的1点,就可找出一系列对应的点和2点。连接这一系列2点即得K2曲线;连接这一系列点所得的曲线称作啮合线,它是这对共轭曲线的接触点在固定坐标系上的轨迹,如曲线[mpa]。
一对共轭曲线也可通过第三条曲线来获得,如曲线3分别与曲线1和曲线2共轭,则1、2两条曲线一定也能共轭。用齿条型刀具加工一对齿轮是其应用实例。
评价一对共轭曲线的优劣,除满足运动要求外,还应考虑啮合特性,如压力角、滑动率、诱导曲率和有无干涉等。
一对共轭曲线的曲率计算可以应用欧拉-萨伐里公式:
[0242-01]式中1和2为轮1和轮2的节圆半径,如图[共轭曲线及其求法]所示, 即图[共轭曲线及其求法]中的PA长,[p]1、[p]2为K1、K2在接触点A的曲率半径,已知[p]1可求得[p]2。当曲线为内凹时,[p]为负值。为了避免产生曲率干涉,应使诱导曲率[242-3]。
参考书目
..李特文著,卢贤占等译:《齿轮啮合原理》第二版,上海科学技术出版社,上海,1984。(.., m, . ,,1968.
施永乐
以上就是网友分享的关于"共轭曲线"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网