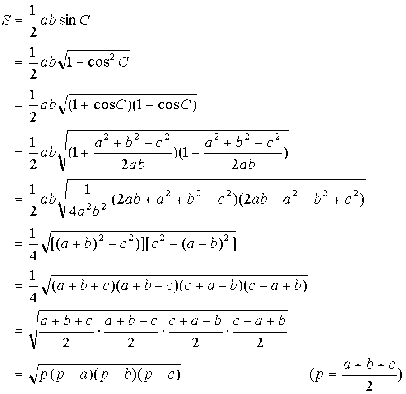第2l卷第3期
2009年6月六盘水师范高等专科学校学报JoumalofLiupanshuiTeachersCollegeV01.21NO.3June2009
用向量法证明海伦公式
杜云
(六盘水师范学院数学系;贵州六盘水553004)
摘要:从数与形的角度对向量进行再认识,通过应用向量方法证明海伦公式。毒进一步阐明了向量是沟通代数与几何的天然桥梁,是一个重要的数学模型,它能为解决问题提供新的方法和视角。
关键词:向量;几何;海伦公式;数形结合
中图分类号:G421文献标识码:A
ToproVe文章编号:1671—055X(2009)03—0063一03Hemn,SFomlula啊tIlU地Ⅵ圮tor
DUYun?
(Mathe啪ticsDep缸ment
Abstract:Recognizedtllevectorof“upanshuiNomalCollege;Uup锄shui,553004,China)geometryandf而malgebmand
abyprovingHeron,sFb瑚uIaanfunherexpounds,Ifshowstharthevectorisnaturalbridgebetweenal霄ebraandPIeometry,arlditi8imDortant
mathematicsstyle,andalsoprovidesthenewmethodandviewtosolvetlleproblems.
Keywords:Vector;geomeny;Heron,sFo硼uIa;combinationbetweenalgebraandgeomeⅡy
向量是现代数学中重要和基本的数学概念之一。它既是几何的研究对象,又是代数的研究对象,是沟通代数、几何的桥梁;有着极其丰富的物理背景和应用背景,是重要的数学模型;具有良好的运算通性、几何的直观性、表述的简洁性和处理问题的一般性,对各种数学问题融会贯通,是一种成熟的、广泛应用的数学工具。适当地把向量方法用于各数学分支,既为我们解决这些数学问题提供了新的方法、增加新的视角,又扩充了学生的数学视野,提高了学生的数学素养,同时也是培养学生创新精神的一种良好方法和有效途径。
随着数学课程改革的深入,向量不仅仅在近代几何、现代数学中有广泛的运用,而且在中学初等几何、三角函数等问题中也体现出不可替代的作用,用向量方法不仅使这些问题简单化,更重要的是为学生提供了一种解决问题的有效方法。通过应用向量来解决平面几何、立体几何和三角函数中的相关问题,让学生感受到向量作为一个成功的数学模型,是由人们在生产、生活中不断抽象、升华、提炼而成的,能很好地激发刚踏入大学校门的大学生的学习兴趣,使他们掌握正确的学习和研究的方法。1对向量的再认识
向量是一个具有几何和代数双重身份的概念,同时向量代数所依附的线性代数是高等数学中一个完整的体系,具有良好的分析方法和完整结构。通过向量的运用对传统问题的分析,可以帮助学生更好地建立代数与几何的联系,也为中学数学向高等数学过渡奠定直观的基础.
向量的原型是力,它是物理对象,用有向线段表示力,使它成了几何对象;引入坐标系后向量又变成了有序实数,从而又变成了代数对象;向量沟通了物理与数学,并具有几何和代数双重身份。在数学中我们习惯用“数”表示代数,“形’’表示几何,向量是数形结合的桥梁,体现了数学的统一性与和谐性。
随着人们对向量认识的深化,向量从3维发展到n维。例如,把所有实系数多项式的全体看成一个多项式空间,这里的多项式都可看成一个向量。在这种情况下,要找出起点和终点甚至画出箭头表示方向是办不到的。这种空间中的向量比几何中的向量要广泛得多,可以是任意数学对象或物理对象,这样,就通过向量把线性代数方法应用到广阔的自然科学领域中去了。因此,向量空间的概念,已成了数学中最基本的概念和线性代数的中心内容,它的理论和方法在自然科学的各领域中得到了广泛的应用。而向量及其线性运算也为“向量空间”这一抽象的概念提供出了一个具体的模型。
例如,对于柯西不等式:0I轨+n2%+…+口。以)2≤@;+口;+…+口:)(612+易;+…+易:)收稿日期:2009—03一03
作者简介:杜云(1982一),男,贵州盘县人,助教,研究方向:高等代数与解析几何。一63—
则c。s<咖≥下』丝竺丝笔竺些√口?+口;+…+口:√易?+易;+…+6:
对于两个n维向量的夹角应考虑lcos<a,6>l≤l,可以利用n维向量的数量积把二者统~起来,设口=(口l+口2+…+a。),6=(易l+易2+…+6。),
这就是著名的柯西不等式,当,l≤3时,可以用有向线段(向量)的数量积公式证明,非常直观、方便。当,l≥4时,不能用向线段来证明,我们可以用纯代数的方法来证明它成立,这也从代数的角度支持了n维向量的合理性,也充分说明了数学的统一性和和谐性。
另一方面,向量是重要的数学模型,用V表示向量的集合,则V对于向量的加法运算构成交换群。(V、R)对于V中向量的加法、实数域R中的实数与向量的乘法(数乘)运算构成线性空间。V中向量的数量积运算可以刻画向量的长度,给V中的向量赋以长度后,(v、R)对于向量的加法、实数与向量的乘法运算构成线性赋范空间。群、线性空间、线性赋范空间都是重要的数学模型,也是抽象代数、线性代数、泛函分析的重要研究对象。因此,向量为理解抽象代数、线性代数、泛函分析提供了基本的数学模型。
把平面和空间看成是一个向量场,还可以培养学生对结构数学的认识,而结构数学是现代数学发展的主要方向。利用参数方程的概念,可以把曲线看作向量函数的轨迹,可以使学生方便地运用微积分于几何的研究和学习,为学生今后学习微分几何、泛函分析等打基础.这里也可以把向量理解为现代数学与初等数学的衔接的组成部分之一。下面介绍向量在平面几何中的一种应用——用向量法证明海伦公式。
2海伦公式
在利用三角形的三个边求面积的问题上,古希腊数学家海伦(Heron)给出的公式:s△=丫页歹=万历=历两,其中a,b,c是三角形三边的长,p=些掣,IS△即为三角形Z
的面积。这就是著名的海伦公式,传说是古代的叙拉古国王希耶隆二世发现的公式,它也叫做秦九韶——诲伦公式。这是因为,我国南宋时期的数学泰斗秦九韶编撰的《数书九章》一书的卷五中曾记载过“三斜求积术”,所谓“术”就是方法,它就是根据三角形三边求三角形的面积的问题。本文日:“问有沙田一段,有三斜,其小斜一十三里。中斜一十四里,大斜一十五里,里法三百步,欲知为田几何”答日:“面积二百一十五顷”其术文是:“以小斜幂并大斜幂,减中斜幂,余,半之。同乘于上,以小斜幂乘大斜幂,减上。余,四约之为实,开平方,得积。”若以大斜记为a,中斜记为6,小斜记为c,秦九韶的方法相当于下面的一般公式:s△:1辟【口:f:一(尘掣)z】这里口≥6≥cY4Z
它虽然与海伦公式形式上不一样,但两者是完全等价的,实质是一样的。故海伦公式也称之为秦九韶——海伦公式。下面我们就运用向量这一有力工具来证明秦九韶——海伦公式。
3海伦公式的向量法证明
例l设△ABc三边长分别为d,6,c,p是半周长,即p:生掣
2
则?叉=√p(p一口)(p一易)(p—c),
一“一证明:如图l,设丽=4,历=6,否=c,I丽l=口,陋l=c,I蕴l=6,
由口拍H=O,可知(口+6)2司2A
利用数量的交换律与分配律得42柏2+2口.6号2
即有4?易=丢(孑。口2一西2)。C
另一方面,由向量的数量积的概念可知
B图l
口礓2一(4?6)2=口262(1一cos2c)=口2易2siIl2c=4s:

故4s:=口2易2一三(c2一口2—62)2(1)
这就是海沦公式,即用△ABC三边长分别为口,6,c来表示△ABC的面积。下面把(1)式代为所要的形式。
4s:=如2一扣彳∥)2=三【坳-(c2彳∥)】【2拼(^口2-∽】_三(口+易㈦又因胪掣,有4《:4p(p一口)(p一易)(p—c)(口+6一c))(c+口一易)(c一口+6)
即s:=p(p一口)(p一易)(p—c)
所以s△=√p(p一口)(p一易)(p—c)
上述证明中关键是将三角形的面积用向量来表示,然后利用向量的运算律将其化简,这样就使几何问题完全代数化了。由于向量运算的规律本身就包含着几何定理的内容,因此利用向量的运算律进行向量的代数运算,实际上就是利用基本的几何定理来进行推理,向量的代数运算本身就是一种几何推理,这样向量就把代数与几何,数与形自然地结合在一起了,因此说向量是沟通代数与几何的一座天然的桥梁。
参考文蚨:
【1】王培甫,张金兰.向量及其应用【M】.北京:高等教育出版社,2005
【2】秦九韶.数书九章新释【M】.合肥:安徽科学技术出版社,1992
【3】胡银伟.向量的由来【J】.数学爱好者(高一籼,2007(3):57
【4】吕林根,许子道.解析几何:第四版【M】.北京:高等教育出版社,2006—65—
用向量法证明海伦公式
作者:
作者单位:
刊名:
英文刊名:
年,卷(期):
被引用次数:杜云, DU Yun六盘水师范学院数学系,贵州,六盘水,553004六盘水师范高等专科学校学报JOURNAL OF LIUPANSHUI TEACHERS COLLEGE2009,21(3)0次
参考文献(4条)
1.王培甫.张金兰 向量及其应用 2005
2.秦九韶 数书九章新释 1992
3.胡银伟 向量的由来 2007(03)
4.吕林根.许子道 解析几何 2006
相似文献(10条)
1.期刊论文 陆金菊.Lu Jinju 试论向量在几何中的应用 -山西广播电视大学学报2010,15(1)
向量在解决数学问题中有着广泛的用途.利用向量知识解决几何问题可以将"定性"研究转变为"定量"分析,使复杂问题简单化.从而,使学生掌握"数形"结合的方法,提高解决问题的能力.
2.期刊论文 徐永红.洪文学.高直 模式特征的几何代数多向量表示方法 -燕山大学学报2010,34(2)
模式表示是模式识别的一个基本问题.传统统计模式识别理论中模式特征一般表示为一个数值向量,并被视作n维欧式空间中的一个点.这种表示方法只利用了一阶特征,容易丢失模式特征间的关联信息和高阶结构.本文首先阐述了几何代数的公理化定义和一些基本概念,然后将传统的模式特征向量表示推广为几何代数空间的多向量表示,接着讨论了该表示的两种特例,最后阐述了基于该多向量表示进行特征提取和分类的一般思想和需要进一步研究的问题.
3.期刊论文 丁自瑞.Din Zirui 向量在几何中的应用 -保山师专学报2005,24(5)
向量,包括平面向量和空间向量,是高中数学新教材的主要内容之一.随着课改的深入,高考命题中向量将是不可缺少的重要命题点,在教学中我们看到,向量在几何中的用途是很大的,向量在处理长度、距离、夹角、垂直、平行等几何问题中占明显优势,向量的使用大大降低了某些题目的难度,简化了运算,它是解决几何问题的有力工具.
4.学位论文 陈雪梅 中学向量课程与教学的研究 2007
向量是高中数学课程的重要内容。向量作为一种不同于数的量,有自己独特的运算结构和系统,学习向量有助于发展学生对“数、量和运算”的认识。向量几何提供了一种认识空间和图形的新方法,使学生初步领略机械化的现代数学思想。向量是现代数学的基本概念之一,可以使师生从一种新的角度诠释许多初等数学知识,并为学习高等数学中线性代数理论奠定基础。
近几年,从数学角度探索向量教与学的研究多是探讨技术进入数学课程后怎样影响学生数学概念的发展以及解题途径的产生。向量概念包括方向和大小两个维度,有几何图像和代数坐标等多种表征方式。这给教学和学生的概念理解都带来一定困难。向量进入我国高中数学课程后,引起广大师生的极大关注和兴趣。但国内数学教育研究领域对向量教学中许多重要而基础的问题一直缺少实证研究。例如普通高中数学课程标准中要求学生“理解平面向量概念”,“能用向量语言表述线线、线面、面面的垂直、平行关系。能用向量方法证明有关线、面位置关系的一些定理。”,“体会向量方法在研究几何问题中的作用”,等等。因此,我们试图通过对向量教学中四个基本问题的探讨来反映当前的现状和问题。
我们首先以SOLO,APOS等教学理论为基础检验学生对向量概念(几何图象和代数坐标)的理解水平,以及与向量概念有关的错误类型。我们选择302名高二学生为被试,利用测试卷、访谈、个案研究作为研究工具。研究发现,对于检验向量概念的测试题,有约占总数22%的学生在几何图像方面达到水平4,约占总数3%的学生在代数符号方面达到水平4,只有约2%的学生在几何图像和代数符号两个方面都达到灵活协调阶段。大多数学生没有建构自由向量概念。学生更倾向于应用向量的几何图像表征处理问题。把向量看作一段距离或一个数是向量错误的主要类型。
其次,我们检验了用向量法处理立体几何度量与位置关系问题的教学效果。以测试卷和调查表为工具,我们对368名高三学生怎样处理能用两种方法(综合法与向量法)解决的立体几何(位置关系与角的度量)问题以及学生对两种方法特征的认识进行了研究。研究结果表明:同时用两种方法处理问题的学生(EV型)人数最多,仅使用综合法(E型)的人数略高于仅使用向量法(V型)的人数。但V类型学生的解法似乎更有效,成功率高于E类型学生。而且EV类型学生的得分结果也表明,向量方法的正确率高于综合法。
我们还分析了两种错误类型——一般性错误与向量错误。对E类型和EV类型学生来说,一般性错误主要出现在逻辑推理方面,其次是技术性错误,误用题目信息,误用定理或定义。对于运用向量方法的学生,V类型学生和EV类型学生(应用向量法部分)的一般性错误类型都是数学语言转换。向量坐标计算错误是向量错误的主要类型。对于两种方法(综合法与向量法)特征的认识,研究表明学生认为综合法的最主要优点是:综合法是解决立体几何问题的基本方法(向量只能处理个别问题)。综合法的最主要缺点是不会做辅助线以及找不到要求的线或角。学生认为向量法的最主要优点是方法简洁有效,向量法的主要缺点是计算繁琐易出错。
第三,我们以皮亚杰的图式理论为基础,从知识关联性的角度研究了教师的向量概念。我们以测试卷、访谈、个案研究为工具,对23名教师进行了调查。结果表明:大多数教师不能以一种系统的观点去看待向量概念及其一些变换,例如,他们对向量概念的理解仅限于教材中的定义——“向量是既有大小又有方向的量”。他们虽然能判断~个线性方程组有无解,但不能表示出解空间的结构。他们认为复数、矩阵与向量概念有许多相似,但看不清几个概念之间的关系。
第四,我们通过对上海、沈阳和石家庄三地1069位教师的问卷调查和其后三位教师的访谈,调查高中教师对向量在高中数学课程中作用的态度,教师相关教学知识的发展途径,教师希望进一步培训的内容,等等。结果表明:立体几何简化论和解题方法的多样性是大多数教师对向量进入高中数学课程的基本认识。
最后,我们通过反思和整合各项研究结果,得出如下结论:(1)教材和教学没有重视培养学生的自由向量概念。(2)立体几何用两种方法(综合法和向量法)处理没有引起学生的思维冲突,但仍受欧氏几何影响较深。(3)大多数教师具有的向量知识以程序性经验为主。(4)囿于自身经验积累和反思,以及同水平经验分享的知识发展途径影响了教师教学内容知识(向量概念)的进一步发展。据此,我们对向量教学、教材编写以及教师培训提出若干建议:(1)教材应明确提出自由向量概念。(2)改进向量定义的叙述方式。(3)教学应展现向量概念从不同的物理情境到数学概念的抽象过程,突出自由向量的概念本质。(4)加强向量的代数坐标表示及运算的教学。(5)探索和推广新的教师教育发展模式势在必行。
5.期刊论文 娄祖安 用向量法证明与动点有关的几何问题 -考试周刊2009,""(39)
随着向量知识进入高中教材,用向量法解几何问题已经成为教师关注的热点问题.本文从与动点有关的几何问题入手,略举数例,探讨直接用向量基本性质和运算律的简便方法证明几何问题的思路和技巧.
6.学位论文 黄光华 高中生对平面向量的认知特点及教学启示 2006
本文通过对高中三个年级的数学高成绩组和低成绩组的15名学生进行了调查、访谈以及个案观察,阐述了中学生对平面向量及其一些概念(模)的认知过程。结果显示,学生对平面向量及其一些概念(模)的理解呈现三个侧面:(1)代数意义上的理解;(2)几何意义上的理解;(3)整体意义上的理解。借助认知心理学的理论,本文详细分析了两组学生在三种理解上的认知特点及其影响因素。调查显示:平面向量是认知的难点,影响学生学习平面向量整篇文章可从四个方面加以分析:(1)实数的相关知识对平面向量表示形式的影响;(2)平面向量的学习是学生认知的重组和深化;(3)教师的教学观点、教学方法对平面向量表示形式的影响;(4)教材体系的编排对学生学习平面向量的影响。研究者还通过个案观察调查了带有不同思维倾向的学生(“代数型”、“几何型”、“平衡型”)在平面向量认知中的现状,并分析了其特点:“代数型”倾向于抽象思维;“几何型”倾向于形象思维;“平衡型”是抽象思维和形象思维均衡发展。
7.期刊论文 王燕 向量在几何题中的应用 -科技信息(学术版)2008,""(28)
在新版的高职教材中,引入了平面向量和空间向量的概念.向量的出现为同学解决几何问题提供了更多、更简单的方法.本文主要从平行、垂直两种位置关系,角度、长度两种度量问题,一共四个方面讨论了向量在几何题目中的应用.
8.期刊论文 刘华 "平面向量"的教学感悟 -商情2009,""(2)
"平面向量"进入高中教材,适应了当今的课程改革.高中几何改革的趋势是几何问题的代数化,向量就为用代数方法研究几何问题提供了强有力的工具,对于它,我们不仅作为一种知识去学习,还要作为一种解题思想去理解,作为一种解题工具去应用,这一点在新教材中尤为明显.本文结合自己的教学实践谈谈对"平面向量"的教学体会.
9.期刊论文 黄丹妹 构造向量解一类几何问题 -广西轻工业2007,23(6)
向量是研究空间解析几何,特别是研究平面和空间直线相关问题的重要工具,而且在数学的其他分支、其他学科也有重要价值.本文将通过构造向量,利用向量的相关知识解答一类几何问题,以感受向量在研究中学数学问题中的重要价值.
10.学位论文 杨巧玲 向量型Sturm-Liouville问题的特征值重数 2008
本文主要是研究向量型Sturm-Liouville问题的特征值重数问题.文章首先证明在满足一定的条件下,当n≥2时,向量型Sturm-Liouville问题有有限个几何重数为n,的特征值.然后得到结论,当n=2时,对于满足一定条件的Q(x),可以找到一个依赖于Q(x)的序数mQ,使得当上述向量型Sturm-Liouville问题的特征值的序数超过mQ时,问题的特征值都是单的.应用这些结论可以推导出两个势问题的谱有有限个公共元素,并且可以估计出两个谱交集元素的个数.最后证明向量型Sturm-Liouville问题的特征值的代数重数和几何重数之间的关系,也就是,若向量型Sturm-Liouville问题的特征值的几何重数为2,则问题的代数重数也为2.
本文链接:http://d.wanfangdata.com.cn/Periodical_lpssfgdzkxxxb200903020.aspx
授权使用:中共汕尾市委党校(zgsw),授权号:3cc3f681-bd69-438b-9766-9dca00986387
下载时间:2010年8月6日
 爱华网
爱华网