为了评估SA方法求得的解,我们把它与用Aarts和Korst[15]的本地搜索过程求得的最佳解和用随机生成过程获得的解比较。用本地搜索过程求得的最佳解为系统成本fc(s)=20452.4和小区数n=13。如成本函数(19)所示,每个小区的固定成本 决定总系统成本。这意味着成本有效设计应该有较少的小区数和每个小区较高的平均话务负载。用SAEON和本地搜索方法求得的最佳解中的话务量柱形图。在小区数也是13这种情况下,随机生成过程获得的解的话务量分布。虚线和实心条分别代表每个小区能提供的话务负载和需要的话务负载。我们观察到用SAEON求得的逼近最优解在能提供的话务负载和需要的话务负载之间取得了好的折衷。与其它两个过程相比,每个小区的话务负载也呈均匀分布。如图4 的最终设计所示,这个设计能满足覆盖要求,同时也努力用最小的小区数和最佳的小区安置适应非一致话务负载。
天线增益和发射功率的逼近最优值可从最佳解中获得。
在最后一步,基站和移动单元的所有参数都要根据所在小区内具体的地形数据和覆盖特征进行调整。从上面两层获得的结果能满足覆盖的质量要求,但并不能提供每个小区的所有预期话务量。在最后一层,Gamst[23]技巧被用来确定要分配的信道数下界。然后进一步应用Dugue-anton[20]的信道分配过程去满足话务要求和避免干扰。
模拟退火方法SAEOM的性能研究分两个方面:解的质量和执行时间[13]。我们把SAEOM求得的次优解比作用本地搜索方法及随机生成过程获得的最优解。如表Ⅱ和Ⅲ所示的四种不同大小的问题都应用了这些方法。
本地搜索算法是一种由Aarts[15]提出的贪婪算法,用本地搜索算法求得的解严重地依赖于初始解。计算时间的上界,即最差情况下的时间复杂度对很多问题而言都不可知[15][13]。给定次数N 对相同的问题用不同的初始值运行本地搜索算法,我们就得到了平均时间,平均CPU时间,最佳结果及进行大量优化获得最佳结果所花的总CPU时间[15] [8]。
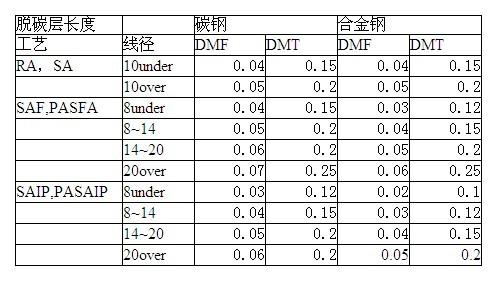
在对同样的问题运行SAEOM10次后就得到了模拟退火算法SAEOM的CPU时间和最佳结果的平均值。
表Ⅱ和Ⅲ比较了这些算法的解。从中可注意到模拟退火方法能在较短的时间内求得较好的解。由于固定小区成本 决定总系统成本,如表Ⅱ所示在SAEOM的平均结果和本地搜索的最佳结果之间没有发现什么显著区别。当话务成本因子 增加时,与表Ⅱ相比,表Ⅲ中的SAEOM的解和本地搜索的解的差别变大。从表Ⅱ和Ⅲ可以看出,每次执行本地搜索所需的CPU时间远远小于模拟退火所需的 CPU时间。但与模拟退火相比,本地搜索需要多得多的时间去得到最优解。
一般情况下模拟退火算法解的质量可以通过调节控制参数(λ,χ,etc)的值,减慢冷却过程和增加马尔可夫链的长度[15]来得到改善。图9显示了应用SAEOM算法时,解的质量和运行时间之间的折衷。成本为 的最终解的质量由如下定义的相当误差ε决定:
ε=
其中 是曾经求得的最佳值。对于大型案例的广泛研究表明一个具有良好质量的解能通过降低λ和增加χ来得到。
本文由深圳家之福搬家公司收集发布,转载请注明出处http://www.jzfbj.com
 爱华网
爱华网