工程问题是一种典型的分数应用题。这类应用题的特点是:题中不给出工作量的具体数量,而用整体“1”来表示;工作效率以单位时间内完成工作总量的几分之几来表示,而后根据工作量、工作效率、和工作时间三者的关系来解答。
基本数量关系式是:
工作量÷工作效率=工作时间
在运用上面数量关系进行解答时,要注意工作量必须与完成这些工作量所需要的时间相对应。
例1、 甲乙两队合作某一项工程,12天可以完成;如果甲队工作2天,乙队工作3天,他们只能完成这项工程的20%。甲乙两队单独完成这项工程,各需多少天?
解法一:
把“甲队工作2天,乙队工作3天,只能完成这项工程的20%”转换成“甲乙两队合作2天,乙再工作1天”。
把这项工程看作单位“1”,甲乙合做1天可完成这项工程的 ,合做2天可完成这项工程的 ×2,从而求得乙的工作效率:
(20%- ×2)÷(3-2)=
乙单独完成这项工程的天数
1÷ =30天
甲队单独完成这项工程的天数
1÷( - )=20天
解法二:
假定甲与乙一样工作3天,完成的工作量为 ×3= ,这时工作量必定超过20%,超过部分 +20%,就是甲队一天的工作量。
甲队单独完成这项工作所需时间
1÷( ×3-20%)=20天
乙队单独完成这项工作所需时间
1÷( - )=30天
例2、 甲乙丙三个车队运输一批货物。甲乙两个车队在6天内运完 ,以后由乙丙两个车队合运2天,完成了余下货物的 ,最后甲乙丙三个车队合运5天才运完。甲队、乙队、丙队单独运输这批货物,各需多少天?
要求甲乙丙三队单独运输,各需多少天,要设法求得甲乙丙三队的工作效率。
甲乙两队的工作效率为 ÷6= ;
乙丙两队的工作效率为(1- )× ÷2= ;
三队合做的工作效率为(1- )×(1- )÷5= 。
由此,可求得甲队、乙队、丙队的工作效率。
1、 甲乙两队的工作效率
÷6=
2、 乙丙两队的工作效率
(1- )× ÷2=
3、 三队合做的工作效率
(1- )×(1- )÷5=
4、 甲队单独运完这批货物所需天数
1÷( - )=60天
5、 乙队单独运完这批货物所需天数
1÷[ -( - )]= 天
6、 丙队单独运完这批货物所需天数
1÷( - )=
例3、 一项工程,原定100人,工作90天完成;工程进行15天后,由于采用先进工具和技术,平均每人工效提高了50%。完成这项工程可提前几天?
要求完成这项工程,可以提前几天,先要求出实际所用的天数;要求实际所用的天数,先要求出完成余下的工程所用的天数。全工程原定100人90天完成,那么,平均每人每天要完成全工程的 ;100人工作15天完成了全工程量的 ×100×15。余下全工程的(1- ×100×15)。采用先进技术后,每人工作效率是:[ ×(1+50%)],进而求得余下的工程所用的天数。
1、 100人工作15天后,还余下全工程的几分之几?
1- ×100×15=
2、 改进技术后,100人1天可以完成这项工程的几分之几?
×(1+50%)×100=
3、 余下的工程要用多少天?
÷ =50天
4、 可提前多少天?
90-15-50=25天
综合算式:
90-15-(1- ×100×15)÷[ ×(1+50%)×100]=25天
例4、 有一水池,装有甲乙两个注水管,下面装有丙管排水。空池时,单开甲管5分钟可注满;单开乙管10分钟可注满。水池注满水后,单开丙管15分钟可将水放完。如果在空池时,将甲乙丙三管齐开,2分钟后关闭乙管,还要几分钟可以注满水池?
分析与解:
先求出甲乙丙三管齐开2分钟后,注满了水池的几分之几,还余下几分之几。再求余下的要几分钟。
1、 三管齐开2分钟,注满了水池的几分之几?
( + - )×2=
2、 还余下几分之几?
1- =
3、 余下的还要几分钟?
÷( - )=4分钟
例5、 一队割麦工人要把两块麦地的麦割去。大的一块麦地比小的一块大一倍。全队成员先用半天时间割大的一块麦地,到下午,他们对半分开,一半仍留在大麦地上,到傍晚时正好把大麦地的麦割完;另一半到小麦地去割,到傍晚时还剩下一小块,这一小块第二天由1人去割,正好1天割完。这个割麦队共有多少人?
分析与解:
把大的一块麦地算作单位“1”,小的一块麦地为 。根据题意,一半成员半天割了 ,一天割了 ,全队成员一天可割 ×2= 。
1、 全队成员一天可割几分之几?
×2=
2、 所剩的一小块面积是几分之几?
-( -1)=
3、 全队有多少人?
(1+ - )÷ =8人
例6、 一项工程,甲工程队每天工作8小时,3天可以完成;乙工程队每天工作9小时,8天可以完成。如果两工程队合作,每天工作6小时,几天可以完成?
分析与解:
要求两队合做,几天可以完成,先要求出甲工程队每小时可以完成全工程的几分之几,乙工程队每小时可以完成全工程的几分之几。
1、 甲工程队每小时可以完成全工程的几分之几?
1÷(8×3)=
2、 乙工程队每小时可以完成全工程的几分之几?
1÷(9×8)=
3、 两队合作几天可以完成
1÷( + )÷6=3天
综合算式:
1÷[1÷(8×3)+1÷(9×8)]÷6=3天

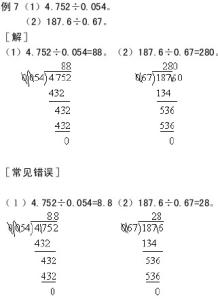
例7、 一件工作,3个男工和4个女工一天能完成 ;3个女工和4个男工一天能完成 。如果由1个女工独做,几天可以完成?
分析与解:
要求由1个女工独做,几天可以完成,先要求得1个女工的工作效率;要求1个女工的工作量,先要求1个男工和2个女工一天的工作量。
“3个男工和4个女工一天能完成 ”和“3个女工和4个男工一天能完成 ”把这句话合并成;“7个男工和7个女工一天能完成这件工作的 + 。”
1、 7个男工和7个女工一天的工作量。
+ =
2、 一个男工和一个女工一天的工作量。
÷7=
3、 一个女工一天的工作量
- ×3=
4、 一个女工独做需要多少天
1÷ =18天
例8、 一项工程,甲独做10天完成,乙独做12天可以完成,丙独做15天完成。现在三人合作甲中途因病休息了几天,结果6天完成任务。甲休息了几天?
如果甲没有休息,那么甲乙丙都工作了6天,完成了工程量的几分之几,超过了几分之几,然后求得甲休息了几天。
1、 三人合做6天,完成了工程量的几分之几?
( + + )×6=
2、 超额完成了工程的几分之几?
-1=
3、 甲休息了几天?
÷ =5天
 爱华网
爱华网