三面角正弦定理 三面角正弦定理-表述 ，三面角正弦定理-证明

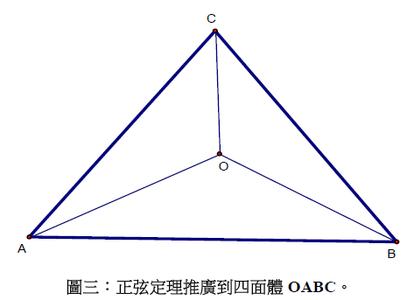
三面角正弦定理是一个数学定理。 是立体几何的基本概念之一，是组成多面体的重要元素。与平面几何中有关三角形的正、余弦定理类似，有关三面角的正、余弦定理是解三面角的重要依据。

正弦定理的证明_三面角正弦定理 -表述：

设三面角∠P-ABC的三个面角∠BPC，∠CPA，∠APB所对的二面角依次为∠PA，∠PB，∠PC，则


Sin∠PA／Sin∠BPC=Sin∠PB／Sin∠CPA=Sin∠PC/Sin∠APB。

正弦定理的证明_三面角正弦定理 -证明：

过A做OA⊥平面BPC于O。过O分别做OM⊥BP于M与ON⊥PC于N。连结AM、AN。


显然，∠PB=∠AMO，Sin∠PB=AO／AM；∠PC=∠ANO，Sin∠PC=AO／AN。


另外，Sin∠CPA=AN／ＡＰ，Sin∠APB=ＡＭ／ＡＰ。


则Sin∠PB／Sin∠CPA＝ＡＯ×ＡＰ／（ＡＭ×ＡＮ）＝Sin∠PC/Sin∠APB。


同理可证Sin∠PA／Sin∠BPC=Sin∠PB／Sin∠CPA。即可得证三面角正弦定理。

正弦定理的证明_三面角正弦定理 -全向量证明

爱华网本文地址 » http://www.aihuau.com/a/8103210103/11805.html