帕斯卡原理_帕斯卡定理 -数学定理
定义
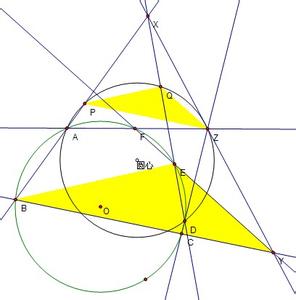
帕斯卡定理指圆锥曲线内接六边形其三对边的交点共线,与布列安桑定理对偶,是帕普斯定理的推广。该定理由法国数学家布莱士·帕斯卡于16岁时提出,是射影几何中的一个重要定理。定义的推广
本定理可推广为:圆锥曲线内接六边形的三双对边(所在直线)的交点共线。证明
引理1:两圆交于A、B,分别过A、B的直线交两圆于C、D,E、F,则CE//DF.画图即证。
引理2:两三角形的对应边都平行,则对应点的连线共点。
证法1.利用相似三角形,采用同一法证明。
证法2.直接应用笛沙格定理。
正式证明:
考察下图即得。
评注:
帕斯卡定理的证法有很多。
还有,反演,射影变换,射影对应等证法。
此法是十分别致,而且十分的初等。
帕斯卡原理_帕斯卡定理 -物理定理
定义
帕斯卡定律:加在密闭液体任一部分的压强,必然按其原来的大小,由液体向各个方向传递。原理的发现
发现定理 1651~1654年,帕斯卡研究了液体静力学和空气的重力的各种效应。
经过数年的观察、实验和思考,综合成《论液体的平衡和空气的重力》一书。提出了著名的帕斯卡定律(或称帕斯卡原理),即加在密闭液体任何一部分上的压强,必然按照其原来的大小由液体向各个方向传递。
原理的意义
著名科学史家沃尔夫称,帕斯卡的这一发现是17世纪力学发展的一个重要里程碑。帕斯卡在此书中详细讨论了液体压强问题。在第一章中,帕斯卡叙述了几种实验,它们的结果表明,任何水柱,不论直立或倾斜,也不论其截面积的大小,只要竖直高度相同,则施加于水柱底部的某一已知面积的活塞上的力也相同。这一个力实际上是液体所受的重力。书中详细叙述了密封容器中的流体能传递压强,讨论了连通器的原理。
帕斯卡利用一个充水的容器,它有两个圆筒形的出口,除此之外,其他部分都封闭。两个出口的截面积相差100倍,在每一个出口的圆筒中放入一个大小刚好适合的活塞,则小活塞上一个人施加的推力等于大活塞上100人所施加的推力,因而可以胜过大活塞上99个人施加的推力,不管这两个出口大小的比例如何,只要施加于两个活塞上的力和两个出口的大小成比例,则水的平衡就可以实现。帕斯卡在书中一一叙述了密闭液体、压强不变、向各方 传递等帕斯卡定律的基本点。
定律的发现
此书是帕斯卡于1653年写成的,但直到他逝世后的第二年----1663年才首次面世。 帕斯卡是在大量观察、实验的基础上,又用虚功原理加以证明才发现了帕斯卡定律的。在帕斯卡做过的大量实验中,最著名的一个是这样的:他用一个木酒桶,顶端开一个孔,孔中插接一根很长的铁管子,将接插口密封好。实验的时候,酒桶中先灌满水,然后慢慢地往铁管子里注几杯水,当管子中的水柱高达几米的时候,就见木桶突然破裂,水从裂缝中向四面八方喷出。 帕斯卡定律的发现,为流体静力学的建立奠定了基础。发展
帕斯卡还在这一定律的基础上提出了连通器的原理和后来得到广泛应用的水压机的最初设想。他又指出器壁上所受的、由于液体重力而产生的压强,仅仅与深度有关;他用实验,并从理论上解释了与此有关的液体静力学佯谬现象。他在一周之内就突击读完了欧几里得《几何原本》的前六本,并还能把它应用于力学。1653年,他进入牛津大学里奥尔学院做工读生。他没有取得学士学位,而是在1663年获得文学硕士学位。应用
帕斯卡定律是流体(气体或液体)力学中,指封闭容器中的静止流体的某一部分发生的压强变化,将毫无损失地传递至流体的各个部分和容器壁。帕斯卡首先阐述了此定律。压强等于作用力除以作用面积。根据帕斯卡原理,在水力系统中的一个活塞上施加一定的压强,必将在另一个活塞上产生相同的压强增量。如果第二个活塞的面积是第一个活塞的面积的10倍,那么作用于第二个活塞上的力将增大为第一个活塞的10倍,而两个活塞上的压强仍然相等。水压机就是帕斯卡原理的实例。它具有多种用途,如液压制动等。帕斯卡还发现:静止流体中任一点的压强各向相等,即该点在通过它的所有平面上的压强都相等。这一事实也称作帕斯卡原理(定律)。
 爱华网
爱华网


