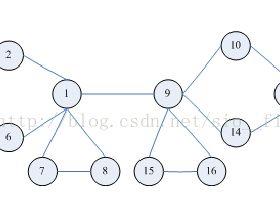
双连通分量定义:在无向连通图中,如果删除该图的任何一个结点都不能改变该图的连通性,则该图为双连通的无向图。一个连通的无向图是双连通的,当且仅当它没有关结点。
定义:在无向连通图中,如果删除该图的任何一个结点都不能改变该图的连通性,则该图为双连通的无向图。一个连通的无向图是双连通的,当且仅当它没有关结点。算法:
1.对图进行先深搜索,计算每一个结点v的先深标号DFN[v]。
2. 计算所有结点v的low[v]是在先深生成树上按照后根遍历的顺序进行的。因此,当访问结点v时它的每个儿子y的low[y]已经计算完毕,这时low[v]取下面三值中最小者:
(1) dfn[v];
(2) dfn[w], 凡是有回退边(v, w)的任何结点w;
(3) low[y],对v的任何儿子y.
双连通分量一个是对点的双连通分量:(即求关节点)当在某一个点v处它的儿子为y low[y] >= dfn[v]即找到了关节点。
(代码怀疑有误,双连通分量栈应该存边而不是点,容易构造出这个代码出错的情况)
void searchB(int start)
{
dfn[start] = low[start] = cnt ++;
stack[top ++] = start;
for ( int i = 0; i < i_vec[start].size(); ++i )
{
if( dfn[i_vec[start][i]] == -1 )
{
father[i_vec[start][i]] = start;
searchB(i_vec[start][i]);
if( low[i_vec[start][i]] >= dfn[start] )
{
while ( true )
{
b_con[b_sn].push_back(stack[top-1]);
point[b_sn][stack[top-1]] = true;
if( stack[--top] == i_vec[start][i] )
break;
}
point[b_sn][start] = true;
b_con[b_sn++].push_back(start);
}
low[start] = min(low[start], low[i_vec[start][i]]);
}
else if( i_vec[start][i] != father[start] )
low[start] = min(low[start], dfn[i_vec[start][i]]);
}
}
另一个是对边的双连通分量:(即求桥)当在某一个点v处它的儿子为y low[y] > dfn[v]即为找到了桥
void searchB(int start)
{
low[start] = dfn[start] = cnt ++;
stack[top++] = start;
for ( int i = 0; i < e_vec[start].size(); ++i )
{
if ( e_visit[e_vec[start][i].mark] )
continue;
e_visit[e_vec[start][i].mark] = true;
if( dfn[e_vec[start][i].to] == -1 )
{
searchB(e_vec[start][i].to);
low[start] = min(low[start], low[e_vec[start][i].to]);
if( low[e_vec[start][i].to] > dfn[start] )
{
from[e_sn] = start;
to[e_sn ++] = e_vec[start][i].to;
while ( top > 0 && stack[top - 1] != e_vec[start][i].to )
Map[stack[--top]] = b_sn;
Map[stack[--top]] = b_sn ++;
}
}
else
low[start] = min(low[start], dfn[e_vec[start][i].to]);
}
}
 爱华网
爱华网