在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式成为雅可比行列式。还有,在代数几何中,代数曲线的雅可比量表示雅可比簇:伴随该曲线的一个群簇,曲线可以嵌入其中。
雅可比行列式_雅可比矩阵 -定义
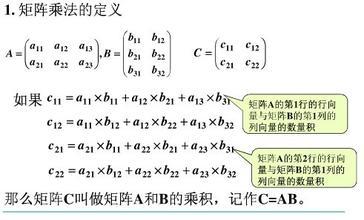
在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。
还有,在代数几何中,代数曲线的雅可比量表示雅可比簇:伴随该曲线的一个群簇,曲线可以嵌入其中。
它们全部都以数学家雅可比命名;英文雅可比量"Jacobian"可以发音为[ja ?ko bi ?n]或者[?? ?ko bi ?n]。
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此,雅可比矩阵类似于多元函数的导数。
雅可比行列式
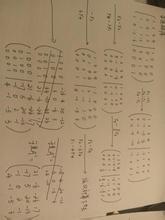
雅可比矩阵定义为向量对向量的微分矩阵,定义式如
下:
见所附jpg图片。
雅可比行列式_雅可比矩阵 -MATLAB
MATLAB中jacobian是用来计算Jacobi矩阵的函数。
syms r l f
x=r*cos(l)*cos(f);
y=r*cos(l)*sin(f);
z=r*sin(l);
J=jacobian([x;y;z],[r l f])
结果:
J =
[ cos(l)*cos(f), -r*sin(l)*cos(f), -r*cos(l)*sin(f)]
[ cos(l)*sin(f), -r*sin(l)*sin(f), r*cos(l)*cos(f)]
[ sin(l), r*cos(l), 0 ]
雅可比行列式_雅可比矩阵 -面积元
关于这个的一般性证明稍微复杂点,现在就给你证明为什么二维的dx(u,v)dy(u,v)=Jdudv成立
证明:对于曲面x=x(u,v),y=y(u,v),取它的微元,即小曲边四边形ABCD,其中
A(u,v),B(u+△u,v),C(u+△u,v+△v),D(u,v+△v),那么这个曲边四边形ABCD可以近似看成是微小向量B(u+△u,v)-A(u,v)和D(u,v+△v)-A(u,v)张成的。利用中值定理可知:

(u+△u,v)-(u,v)=Mdu
(u,v+△v)-(u,v)=Ndv
这里的M,N是偏导数的形式,不好打出,你可以自己算出来,很简单的。
当变化量很小时,我们把(u+△u,v)-(u,v)近似看成dx(u,v),(u,v+△v)-(u,v)看成dy(u,v),所以,
dx(u,v)dy(u,v)=M*Ndudv
而其中的M*N刚好就是二维Jacobi行列式的展开形式。
由此问题得证。
 爱华网
爱华网