双曲正弦函数是双曲函数的一种。记作sinh,也可简写成sh。双曲正弦函数和双曲余弦函数是双曲函数中最基本的两种,由这两个函数可推导出双曲正切函数等等。
正弦函数_双曲正弦函数 -基本定义
双曲函数(hyperbolicfunction)可借助指数函数定义Sinh_cosh_tanh双曲正弦shz=(e^z-e^(-z))/2⑴
双曲余弦
chz=(e^z+e^(-z))/2⑵
双曲正切
thz=shz/chz=(e^z-e^(-z))/(e^z+e^(-z))⑶
双曲余切
cthz=chz/shz=(e^z+e^(-z))/(e^z-e^(-z))⑷
双曲正割
schz=1/chz⑸
双曲余割
xh(z)=1/shz⑹
其中,指数函数(exponentialCsch_sech_cothfunction)可由无穷级数定义
e^z=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…⑺
双曲函数的反函数(inversehyperbolicfunction)分别记为arshz、archz、arthz等。
正弦函数_双曲正弦函数 -基本介绍
在数学中,双曲函数类似于常见的三角函数(也叫圆函数)。基本双曲函数是双曲正弦“sinh”,双曲余弦“cosh”,从它们导出双曲正切“tanh”等。也类似于三角函数的推导。反函数是反双曲正弦“arsinh”(也叫做“arcsinh”或“asinh”)以此类推。双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程。
双曲函数接受实数值作为叫做双曲角的自变量。在复分析中,它们简单的是指数函数的有理函数,并因此是完整的。射线出原点交双曲线x^2-y^2=1于点(cosha,sinha),这里的a被称为双曲角,是这条射线、它关于x轴的镜像和双曲线之间的面积。定义
双曲函数(HyperbolicFunction)包括下列六种函数:
sinh/双曲正弦:sinh(x)=[e^x-e^(-x)]/2
cosh/双曲余弦:cosh(x)=[e^x+e^(-x)]/2
tanh/双曲正切:tanh(x)=sinh(x)/cosh(x)=[e^x-e^(-x)]/[e^x+e^(-x)]
coth/双曲余切:coth(x)=cosh(x)/sinh(x)=[e^x+e^(-x)]/[e^(x)-e^(-x)]
sech/双曲正割:sech(x)=1/cosh(x)=2/[e^x+e^(-x)]
csch/双曲余割:csch(x)=1/sinh(x)=2/[e^x-e^(-x)]
其中,
e是自然对数的底
e≈2.718281828459045...=1/0!+1/1!+1/2!+1/3!+1/4!+1/5!...+1/n!+...
e^x表示e的x次幂,展开成无穷幂级数是:
e^x=x^0/0!+x^1/1!+x^2/2!+x^3/3!+x^4/4!+x^5/5!...+x^n/n!+...
如同点(cost,sint)定义一个圆,点(cosht,sinht)定义了右半直角双曲线x^2y^2=1。这基于了很容易验证的恒等式
cosh^2(t)-sinh^2(t)=1
和性质t>0对于所有的t。
参数t不是圆角而是双曲角,它表示在x轴和连接原点和双曲线上的点(cosht,sinht)的直线之间的面积的两倍。
函数coshx是关于y轴对称的偶函数。
函数sinhx是奇函数,就是说-sinhx=sinh(-x)且sinh0=0。
实变双曲函数
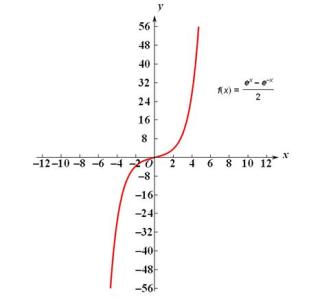
y=sh(x).定义域:R.值域:R.奇函数.函数图像为过原点并且穿越Ⅰ,Ⅲ象限的严格单调递增曲线,当x->+∞时是(1/2)e^x的等价无穷大.函数图像关于原点对称。
y=ch(x).定义域:R.值域:[1,+∞).偶函数.函数图像是悬链线,最低点是(0,1),在Ⅰ象限部分是严格单调递增曲线,当x->+∞时是(1/2)e^x的等价无穷大.函数图像关于y轴对称。
y=th(x).定义域:R.值域:(-1,1).奇函数.函数图像为过原点并且穿越Ⅰ,Ⅲ象限的严格单调递增曲线.其图像被限制在两渐近线y=1和y=-1之间.lim[x->+∞,tanh(x)=1],lim[x->-∞,tanh(x)=-1]。
y=cth(x).定义域:{x|x≠0}.值域:{x||x|>1}.奇函数.函数图像分为两支,分别在Ⅰ,Ⅲ象限,函数在(-∞,0)和(0,+∞)分别单调递减.垂直渐近线为y轴,两水平渐近线为y=1和y=-1.lim[x->+∞,coth(x)=1],lim[x->-∞,coth(x)=-1]。
y=sch(x).定义域:R.值域:(0,1].偶函数.最高点是(0,1),函数在(0,+∞)严格单调递减.x轴是其渐近线.lim[x->;∞,sech(x)]=0.
y=xh(x).定义域:{x|x≠0}.值域:{x|x≠0}.奇函数.函数图像分为两支,分别在Ⅰ,Ⅲ象限,函数在(-∞,0)和(0,+∞)分别单调递减.垂直渐近线为y轴,两水平渐近线为x轴.lim[x->;∞,csch(x)]=0.
双曲函数名称的变更:sh也叫sinh,ch也叫cosh,th也叫tanh,cth也叫coth,sch也叫sech,xh也叫csch。
定义
双曲正弦:sh(z)=[e^z-e^(-z)]/2
双曲余弦:ch(z)=[e^z+e^(-z)]/2
性质
解析性:shz,chz是全平面的解析函数
周期性:shz,chz是周期函数,周期为2πi,这是完全不同于实变函数中的性质
反双曲函数
反双曲函数是双曲函数的反函数.它们的定义为:
arcsh(x)=ln[x+sqrt(x^2+1)]
arcch(x)=ln[x+sqrt(x^2-1)]
arcth(x)=ln[sqrt(1-x^2)/(1-x)]=ln[(1+x)/(1-x)]/2
arccth(x)=ln[sqrt(x^2-1)/(x-1)]=ln[(x+1)/(x-1)]/2
arcsch(x)=±ln[1+sqrt(1-x^2)/x]
arcxh(x)=ln[1-sqrt(1+x^2)/x],如果x<0
ln[1+sqrt(1+x^2)/x],如果x>0
其中,
sqrt为squareroot的缩写,即平方根
正弦函数_双曲正弦函数 -三角函数
双曲函数与三角函数有如下的关系:*sinhx=-i*sin(i*x)
*coshx=cos(i*x)
*tanhx=-i*tan(i*x)
*cothx=i*cot(i*x)
*sechx=sec(i*x)
*cschx=i*csc(i*x)
i为虚数单位,即i*i=-1
正弦函数_双曲正弦函数 -相关信息
与双曲函数有关的恒等式如下:ch^2(x)-sh^2(x)=1
cth^2(x)-xh^2(x)=1
th^2(x)+sch^2(x)=1
加法公式
sinh(x+y)=sinh(x)*cosh(y)+cosh(x)*sinh(y)
cosh(x+y)=cosh(x)*cosh(y)+sinh(x)*sinh(y)
tanh(x+y)=[tanh(x)+tanh(y)]/[1+tanh(x)*tanh(y)]
coth(x+y)=(1+coth(x)*coth(y))/(coth(x)+coth(y))
减法公式
sinh(x-y)=sinh(x)*cosh(y)-cosh(x)*sinh(y)
cosh(x-y)=cosh(x)*cosh(y)-sinh(x)*sinh(y)
tanh(x-y)=[tanh(x)-tanh(y)]/[1-tanh(x)*tanh(y)]
coth(x-y)=(1-coth(x)*coth(y))/(coth(x)-coth(y))
二倍角公式
sinh(2x)=2*sinh(x)*cosh(x)
cosh(2x)=cosh^2(x)+sinh^2(x)=2*cosh^2(x)-1=2*sinh^2(x)+1
tanh(2x)=2tanh(x)/(1+tanh^2(x))
coth(2x)=(1+coth^2(x))/2coth(x)
三倍角公式
sinh(3x)=3sinh(x)+4sinh^3(x)
cosh(3x)=4cosh^3(x)-3cosh(x)
半角公式
cosh^2(x/2)=(cosh(x)+1)/2
sinh^2(x/2)=(cosh(x)-1)/2
tanh(x/2)=(cosh(x)-1)/sinh(x)=sinh(x)/(cosh(x)+1)
coth(x/2)=sinh(x)/(coth(x)-1)=(coth(x)+1)/sinh(x)
德莫佛公式
(cosh(x)±sinh(x))^n=cosh(nx)±sinh(nx)
双曲函数的恒等式都在圆三角函数有相应的公式。Osborn'srule指出:将圆三角函数恒等式中,圆函数转成相应的双曲函数,有两个sinh的积时(包括coth^2(x),tanh^2(x),csch^2(x),sinh(x)*sinh(y))则转换正负号,则可得到相应的双曲函数恒等式。如
三倍角公式
sin(3*x)=3*sin(x)+4*sin^3(x)
sinh(3*x)=3*sinh(x)+4*sinh^3(x)
正弦函数_双曲正弦函数 -?导数介绍
(sinh(x))'=cosh(x)(cosh(x))'=sinh(x)
(tanh(x))'=sech^2(x)
(coth(x))'=-csch^2(x)
(sech(x))'=sech(x)tanh(x)
(csch(x))'=-csch(x)coth(x)
(arcsinh(x))'=1/sqrt(x^2+1)
(arccosh(x))'=1/sqrt(x^2-1)(x>1)
(arctanh(x))'=1/(1-x^2)(|x|<1)
(arccoth(x))'=1/(1-x^2)(|x|>1)
正弦函数_双曲正弦函数 -不定积分
∫sinh(x)dx=cosh(x)+c∫cosh(x)dx=sinh(x)+c
∫sech^2(x)dx=tanh(x)+c
∫csch^2(x)dx=-coth(x)+c
∫sech(x)tanh(x)dx=-sech(x)+c
∫csch(x)coth(x)dx=-csch(x)+c
∫tanh(x)dx=ln(cosh(x))+c
∫coth(x)dx=ln|sinh(x)|+c
∫sech(x)dx=arctan(sinh(x))+c=2arctan(e^x)+c1=2arctan(tanh(x/2))+c2
∫csch(x)dx=ln|coth(x)-csch(x)+c=ln|tanh(x/2)|+c
∫[1/sqrt(x^2+1)]dx=arcsinh(x)+c=ln(x+sqrt(x^2+1))+c
∫[1/sqrt(x^2-1)]dx=sgn(x)arccosh|x|+c=ln|x+sqrt(x^2-1)|+c
(sgn是符号函数.sgn(x)=x/|x|,x≠0;sgn(x)=0,x=0)
正弦函数_双曲正弦函数 -段级数表示
sinh(z)=z+z^3/3!+z^5/5!+z^7/7!+...+z^(2k-1)/(2k-1)!+...(z∈C)cosh(z)=1+z^2/2!+z^4/4!+z^6/6!+...+z^(2k)/(2k)!+...(z∈C)
arcsinh(z)=z-(1/6)z^3+(3/40)z^5-(5/112)z^7+...+(-1)^k[(2k-1)!!/(2k)!!][z^(2k+1)/(2k+1)]+...(|z|<1)
arctanh(z)=z+z^3/3+z^5/5+z^7/7+...+z^(2k-1)/(2k-1)+...(|z|<1)
正弦函数_双曲正弦函数 -实际应用
双曲函数并非单纯是数学家头脑中的抽象,在物理学众多领域可找到丰富的实际应用实例。阻尼落体
在空气中由静止开始下落的小石块既受重力的作用又受到阻力的作用。设小石块的质量为m,速度为v,重力加速度为g,所受空气阻力假定与v2正比,阻尼系数为μ。设初始时刻小石块静止。求其小石块运动速度与时间的关系。
解:
小石块遵循的运动方程为
mdv/dt=mg
 爱华网
爱华网