艾兹格・W・迪科斯彻(Edsger Wybe Dijkstra,1930年5月11日~2002年8月6日)荷兰人。计算机科学家,提出著名的迪杰斯特拉算法,获得过素有计算机科学界的诺贝尔奖之称的图灵奖。
斯特拉_迪杰斯特拉 -迪杰斯特拉
(艾兹格・W・迪科斯彻)Edsger Wybe Dijkstra(1930年5月11日~2002年8月6日)
荷兰计算机科学家,毕业就职于荷兰Leiden大学,早年钻研物理及数学,而后转为计算学。曾在1972年获得过素有计算机科学界的诺贝尔奖之称的图灵奖, 之后,他还获得过1974年AFIPS Harry Goode Memorial Award、1989年ACM SIGCSE计算机科学教育教学杰出贡献奖、以及2002年ACM PODC最具影响力论文奖。
艾兹格・W・迪科斯彻
曾经提出“goto有害论”信号量和PV原语,解决了有趣的“哲学家聚餐”问题。于2002年8月6日在荷兰Nuenen自己的家中与世长辞。终年72岁。
艾兹格・W・迪科斯彻在离散数学中的贡献包括:
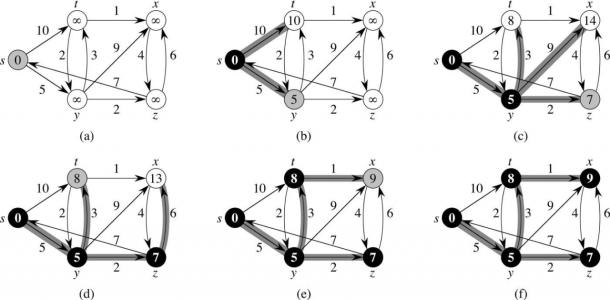
提出了目前离散数学应用广泛的最短路径算法(Dijkstra's Shortest Path First Algorithm)
迪杰斯特拉算法用于求解一个有向图(也可以是无向图,无向图是有向图的一种特例)的一个点(称之为原点)到其余各点(称之为周边点)的最短路径问题。算法构思很是巧妙(我这么认为),简直达到了“无心插柳柳成荫”的境界。算法本身并不是按照我们的思维习惯――求解从原点到第一个点的最短路径,再到第二个点的最短路径,直至最后求解完成到第n个点的最短路径,而是求解从原点出发的各有向路径的从小到大的排列(如果这个有向图中有环1-2-3-1算法岂不是永无终结之日了??!!),但是算法最终确实得到了从原点到图中其余各点的最短路径,可以说这是个副产品,对于算法的终结条件也应该以求得了原点到图中其余各点的最短路径为宜。清楚了算法的这种巧妙构思后,理解算法本身就不是难题了。
算法把一个图(G)中的点划分成了若干部分:
1):原点(v);
2):所有周边点(C);
另外有一个辅助集合S,从v到S中的点的最短路径已经求得。S的最初状态是空集。
这样就可以进一步划分图(G):
1):原点(v);
2):已求出v至其最短路径的周边点(S);
3):尚未求出v至其最短路径的周边点(Other=C-S);
算法的主体思想:
A、找到v――Other所有路径中的的最短路径vd=v――d(Other的一个元素);
B、找到v――S――Other所有路径中的的最短路径vi=v――i(Other的一个元素);
C、比较vd和vi如果vd<=vi则将d加入S且从Other中删除,否则将i加入S且从Other中删除。
重复以上步骤直至Other为空集。
我们求得的最短路径是升序排列的,那为什么下一条最短路径就存在于v――Other或v――S――Other之中呢,难道不能存在于v――Other――Other之中吗??当然不能,因为假设是存在于v――Other――Other之中,那么肯定有一条比这条路径更短的路径v――Other我们没找到呢!
<伪码>
在下面的算法中,u:=Extract_Min(Q)在在顶点集Q中搜索有最小的d【u】值的顶点u。这个顶点被从集合Q中删除并返回给用户。
1function Dijkstra(G, w, s)
2 for each vertex v in V【G】 // 初始化
3 d【v】 := infinity
4 previous【v】 := undefined
5 d【s】 := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijstra算法主体
9 u := Extract_Min(Q)
10 S := S union
11 for each edge (u,v) outgoing from u
12 if d【v】 > d【u】 + w(u,v) // 拓展边(u,v)
13 d【v】 := d【u】 + w(u,v)
14 previous【v】 := u
如果我们只对在s和t之间寻找一条最短路径的话,我们可以在第9行添加条件如果满足u=t的话终止程序。
现在我们可以通过迭代来回溯出s到t的最短路径
1 S := empty sequence
2 u := t
3 while defined u
4 insert u to the beginning of S
5 u := previous【u】
现在序列S就是从s到t的最短路径的顶点集.
<时间复杂度>
我们可以用大O符号将Dijkstra算法的运行时间表示为边数m和顶点数n的函数。
Dijkstra算法最简单的实现方法是用一个链表或者数组来存储所有顶点的集合Q,所以搜索Q中最小元素的运算(Extract-Min(Q))只需要线性搜索Q中的所有元素。这样的话算法的运行时间是O(n2)。
对于边数少于n2的稀疏图来说,我们可以用邻接表来更有效的实现Dijkstra算法。同时需要将一个二叉堆或者斐波纳契堆用作优先队列来寻找最小的顶点(Extract-Min)。当用到二叉堆的时候,算法所需的时间为O((m+n)log n),斐波纳契堆能稍微提高一些性能,让算法运行时间达到O(m + n log n)。
斯特拉_迪杰斯特拉 -相关条目
张大方
谢冬青
闵应骅
杨金民
郭卫锋
申煜湘
鲁春初
 爱华网
爱华网


