发布时间:2018年04月10日 18:39:27分享人:黑桃先生来源:互联网23
全微分方程是常微分方程的一种,它在物理学和工程学中广泛使用。
全微分方程_全微分方程 -简介
全微分方程若微分形式的一阶方程P(x,y)dx+Q(x,y)dy=0的左端恰好是一个二元函数U(x,y)的全微分,即dU(x,y)=P(x,y)dx+Q(x,y)dy
则称Pdx+Qdy=0为全微分方程或恰当微分方程,显然,这时该方程的通解为U(x,y)=C(C是任意常数).
全微分方程_全微分方程 -详解

根据二元函数的全微分求积定理:设开区域G是一单连通域,函数P(x,y),Q(x,y)在G内具有一阶连续偏导数,则P(x,y)dx+Q(x,y)dy在G内为某一函数u(x,y)的全微分的充要条件是,在G内恒成立.
全微分方程的判断:
P(x,y)dx+Q(x,y)dy=0是全微分方程的充分必要条件是。
在区域G内恒成立,且当此条件满足时,方程通解为u(x,y)=P(x,y)dx+Q(x,y)=C
爱华网本文地址 » http://www.aihuau.com/a/8103260103/35739.html
更多阅读

罗贯中(约1330—约1400),汉族,名本,字贯中,号湖海散人。他的籍贯一说是太原(今山西太原),一说是东原(今山东东平),一说是钱塘(今浙江杭州) ,不可确考。但是,近年来由于在山西省祁县河湾村发现了罗贯中之家谱,以及个人使用的印章,故基本可以确定其

全聚德创建于1864年(清朝同治三年), 至今已有140年的历史,是中华著名老字号企业,也是中国首例服务类“中国驰名商标”。 全聚德跨越了三个世纪,经历了晚清衰亡、民国建立、北洋军阀统治、全民族抗战、新民主主义革命几个重大历史时期;新中

重庆美全置业有限公司是主要经营房地产开发、房屋销售的地产公司,2012年5月,因与SOHO中国的建筑版权之争而走入公众视线。美全22世纪_重庆美全置业有限公司 -简介重庆美全置业有限公司主要经营:房地产开发(凭相关资质证书执业);房屋销售
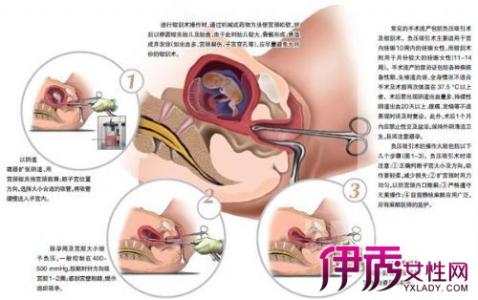
子宫全切术一般采用开腹方式,开腹子宫切除术是非常经典的治疗子宫肌瘤的手术方式,通过切除子宫,从而彻底杜绝了再次生长肌瘤的可能。但失去子宫的同时也带来其他很多的问题,例如:无法生育,内分泌系统的紊乱,心理、情绪上的改变等等。本文主

离婚前规则优酷_优酷全娱乐 -节目编排由2013年3月25日开始,每周一至周五上午十时播出。《小灿大猜想》是《优酷全娱乐》其中一个环节,安排在周五播放,由小灿参与演出。小灿将以其百变形象,扮演娱乐新闻中的人物。离婚前规则优酷_优酷全

 爱华网
爱华网



