在数学中,指数积分是函数的一种,它不能表示为初等函数。
指数函数积分_指数积分 -定义
对任意实数,指数积分有下定义:
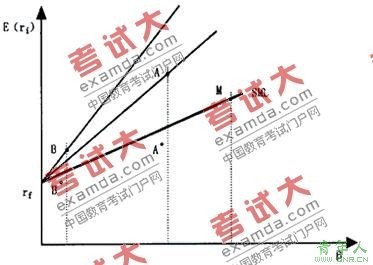
E1函数(顶)和Ei函数(底)。Ei(x)=∫e^t/t dt (-∞~x),这个积分必须用柯西主值来解释。
如果自变量是复数的情形,这个定义就变得模棱两可了 。为了避免歧义,我们使用以下的记法:
E1(x)=∫e^(-t)/t dt (z~+∞) (|ARG(z)|<π)
如果Re(z)>0,则
E1(z)=∫e^(-tz)/t dt (1~+∞) (Re(z)>0)
其中,
Ei(-x±i0)=-E1(x)减加iπ
-Ei(x)=(Ei(-x+i0)+E1(-x-i0))/2
指数函数积分_指数积分 -性质
收敛级数Ei(x)幂级数展开-
-
E1(x)幂级数展开-
-
其中γ是欧拉常数。渐进(发散)级数
自变量的值较大时,用以上的收敛级数来计算指数积分是困难的。在这种情况下,我们可以使用发散(或渐近)级数:
渐进级数-
-
-指数和对数的表现
E1在自变量较大时的表现类似指数函数,自变量较小时类似对数函
数。
大小关系-
-
-
这个不等式的左端在图中用红色曲线来表示,中间的黑色曲线是E1(x),不等式的右端用蓝色曲线来表示。与其它函数的关系
指数积分与对数积分li(x)的关系:
li(x) = Ei (ln (x))x≠ 1
另外一个有密切关系的函数,具有不同的积分限:
E1(x)=∫e^(-tx)/t dt (1~+∞) =∫e^(-t)/t dt (x~+∞)
可以延伸到负数:
Ei(-x)=-E1(x)
我们可以把两个函数都用整函数来表示:
Ein(x)=∫(1-e^(-t))/t dt (0~x)=∑(-1)^(k-1)x^k/(k*k!) (1~∞)
此函数的性质:
E1(z)=-γ-ln(z)+Ein(z) (|Arg(z)|<π)
Ei(x)=γ+ln(x)-Ein(-x) (x>0)
指数积分还可以推广为:
En(x)=∫e^(-tx)/t^n dt (1~+∞)
函数En与E1的导数有以下简单的关系:
En'(z)=-E(n-1)(z) (|Arg(z)|<π ,n>0)
然而,这里假设了n是整数;复数n的推广还没有在文献中报导,虽然这种推广是有可能的。
从定义中可以看出,指数积分与三角积分之间的关系:
E1(ix)=-π/2+S1(x)-i*Ci(x)(x>0)
图中的黑色和红色曲线分别描述了E1(x)的实数和虚数部分。
 爱华网
爱华网