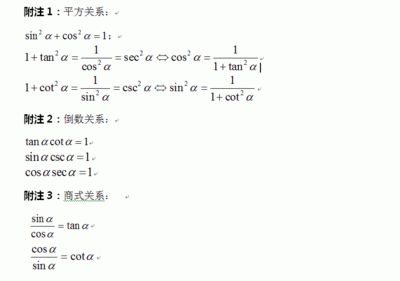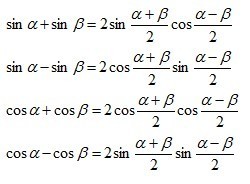在数学中,三角函数(也叫做圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为单位圆上的各种线段的长度。更现代的定义把它们表达为无穷级数或特定微分方程的解,允许它们扩展到任意正数和负数值,甚至是复数值。常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或者计算得出,称为三角恒等式。
三角函数_三角函数 -概述
三角函数: 正弦, 余弦, 正切, 正割, 余割, 余切三角函数在数学中属于初等函数里的超越函数的一类函数。它们本质上是任意角的集合与一个比值的集合的变量之间的映射。由于三角函数具有周期性,所以并不具有单射函数意义上的反函数。三角函数在复数中有重要的应用,在物理学中也是常用的工具。由于三角函数的周期性,它并不具有单值函数意义上的反函数。
三角函数在复数中有较为重要的应用。在物理学中,三角函数也是常用的工具。
它有六种基本函数(初等基本表示):
函数名分别是:正弦、余弦、正切、余切、正割、余割
三角函数_三角函数 -基本函数
函数 简写 关系正弦 Sine sin余弦 Cosine cos正切 Tangent tan(或tg)余切cotangent cot(或 ctg、ctn)正割secantsec余割cosecant csc(或 cosec)三角函数_三角函数 -少用函数
除六个基本函数,历史上还有下面六个函数: 函数 关系正矢余矢
半正矢
半余矢
外正割
外余割
三角函数_三角函数 -历史
随着认识到相似三角形在它们的边之间保持相同的比率,就有了在三角形的边的长度和三角形的角之间应当有某种标准的对应的想法。就是说对于任何相似三角形,(比如)斜边和剩下的两个边的比率都是相同的。如果斜边变为两倍长,其他边也要变为两倍长。三角函数表达的就是这些比率。
研究三角函数的有尼西亚的喜帕恰斯(公元前180-125年)、埃及的托勒密(公元90-180年)、Aryabhata(公元476-550年),Varahamihira、婆罗摩笈多、花拉子密、Abū al-Wafā' al-Būzjānī、欧玛尔・海亚姆、婆什迦罗第二、Nasir al-Din al-Tusi、Ghiyath al-Kashi(14世纪)、Ulugh Beg(14世纪)、约翰・缪勒(1464)、Rheticus和 Rheticus 的学生 Valentin Otho。
Madhava of Sangamagramma(约1400)以无穷级数的方式做了三角函数的分析的早期研究。欧拉的《无穷微量解析入门》(Introductio in Analysin Infinitorum)(1748)对建立三角函数在欧洲的分析处理做了最主要的贡献,他定义三角函数为无穷级数,并表述了欧拉公式,还有使用接近现代的简写 sin.、cos.、tang.、cot.、sec. 和 cosec.。
三角函数_三角函数 -直角三角定义
坐标系直角三角形中
在直角三角形中仅有锐角三角函数的定义。
1.一个锐角的正弦是它的对边与斜边的比值。在图中,sinA = 对边/斜边 = a/h。
2.一个锐角的余弦是它的邻边与斜边的比值。在图中,cosA= 邻边/斜边 = b/h。
3.一个锐角的正切是它的对边与邻边的比值。在图中,tanA = 对边/邻边 = a/b。
直角坐标系中设α是平面直角坐标系xOy中的一个象限角,
函数是角的终边上一点,
函数是P到原点O的距离,则α的六个三角函数定义为:
函数名定义函数名定义正弦
余弦
正切
余切
正割
余割
三角函数_三角函数 -单位圆定义
单位圆
六个三角函数也可以依据半径为一中心为原点的单位圆来定义。单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和 π/2 弧度之间的角。它也提供了一个图像,把所有重要的三角函数都包含了。根据勾股定理,单位圆的等式是:
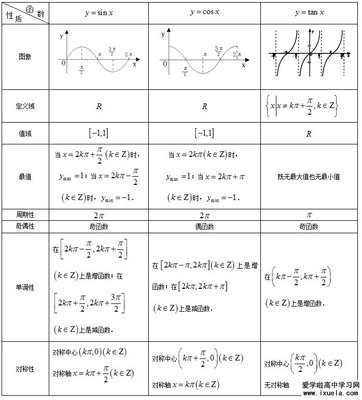
。图像中给出了用弧度度量的一些常见的角。逆时针方向的度量是正角,而顺时针的度量是负角。设一个过原点的线,同 x 轴正半部分得到一个角 θ,并与单位圆相交。这个交点的 x 和 y 坐标分别等于 cos θ 和 sin θ。图像中的三角形确保了这个公式;半径等于斜边且长度为1,所以有 sin θ = y/1 和 cos θ = x/1。单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于 1的一种查看无限个三角形的方式。对于大于 2π 或小于 ?2π 的角度,可直接继续绕单位圆旋转。在这种方式下,正弦和余弦变成了周期为 2π的周期函数:对于任何角度 θ 和任何整数k。
周期函数的最小正周期叫做这个函数的“基本周期”(primitive period)。正弦、余弦、正割或余割的基本周期是全圆,也就是 2π 弧度或 360 度;正切或余切的基本周期是半圆,也就是 π 弧度或 180 度。上面只有正弦和余弦是直接使用单位圆定义的,其他四个三角函数可以定义为:
在正切函数的图像中,在角 kπ 附近变化缓慢,而在接近角 (k 1/2)π 的时候变化迅速。正切函数的图像在 θ = (k 1/2)π 有垂直渐近线。这是因为在 θ 从左侧接进 (k 1/2)π 的时候函数接近正无穷,而从右侧接近 (k 1/2)π 的时候函数接近负无穷。另一方面,所有基本三角函数都可依据中心为 O 的单位圆来定义,类似于历史上使用的几何定义。特别是,对于这个圆的弦 AB,这里的 θ 是对向角的一半,sin(θ) 是 AC (半弦),这是印度的 Aryabhata(AD 476
 爱华网
爱华网