开方(rooting),指求一个数的方根的运算,为乘方的逆运算(参见“方根”词条),在中国古代也指求二次及高次方程(包括二项方程)的正根。数a 的n(n为自然数)次方根指的是n方幂等于a的数,也就是适合b的n次方=a的数b。在复数范围内,无论n是奇数或偶数,任一个非零的复数的 n次方根都有n个。举例 例如计算987654321987654321的五次算术根,就算到小数点后四位。这种方法可以自动调节,第一步与第三步取值偏大,但是计算出来以后输出值会自动转小;第二步,第四步输入值偏小,输出值自动转大。
kaifang_开方 -基本定义
开方(rooting),指求一个数的方根的运算,为乘方的逆运算(参见“方根”词条),在中国古代也指求二次及高次方程(包括二项方程)的正根。
kaifang_开方 -方根
开方
数a 的n(n为自然数)次方根指的是n方幂等于a的数,也就是适合b的n次方=a的数b。例如16的4次方根有2和-2。一个数的2 次方根称为平方根;3次方根称为立方根。各次方根统称为方根。求一个指定的数的方根的运算称为开方。一个数有多少个方根,这个问题既与数的所在范围有关,也与方根的次数有关。在实数范围内,任一实数的奇数次方根有且仅有一个,例如8的3次方根为2,-8的 3次方根为-2 ;正实数的偶数次方根是两个互为相反数的数,例如16的4次方根为2和-2;负实数不存在偶数次方根;零的任何次方根都是零。在复数范围内,无论n是奇数或偶数,任一个非零的复数的 n次方根都有n个。如果复数z=r(cosθ+ i sinθ),r=|z|,那么它的n个n次方根是,k=0,1,2…,n-1。
kaifang_开方 -方法
数字4开方后就是2,2就是它开方的结果
这个用两个相同数字表示一个数的这个数字叫做开方
4=2x2 4等于2×2
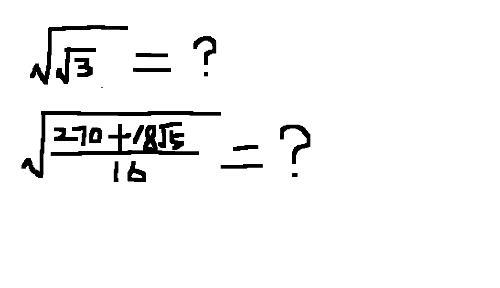
9=3x3 9 等于3×3
16=4x4
25=5x5
36=6x6
49=7x7
64=8x8
81=9x9
100=10x10
2,3,4,5,6,7,8,9,10就是4和9,16,25,36,49,64,81,100开方后的数
关于 任意数 开任意次方的 公式:设被开方数为A,开次方数为B。C为变量
开方
首次 C取值为1 带入A,B常量计算结果 并用计算结果值替换公式中的变量 C 再次计算结果,再次替换,当C=公式计算结果值 此时C即为根 循环步骤受开方数字长度影响,此法也可笔算进行。采用的是牛顿迭代法。且 A B 可为小数,分数,负数,此法为逐次逼近法。可简单的实现编程。但是注意:不能计算负数开偶数次方。
下面为:代入法
1、把被开方的整数部分从个位起向左每隔n位为一节,用撇号分开;
2、根据左边第一节里的数,求得开n次算术根的最高位上的数,假设这个数为a;
3、从第一节的数减去求得的最高位上数的n次方,在它们的差的右边写上第二节数作为第一个余数;
4、用第一个余数除以n(10a)^(n-1),所得的整数部分试商(如果这个最大整数大于或等于10,就用9做试商);
5、设试商为b。如果(10a+b)^n-(10a)^n小于或等于余数,这个试商就是n次算术根的第二位;如果(10a+b)^n-(10a)^n大于余数,就把试商逐次减1再试,直到(10a+b)^n-(10a)^n小于或等于余数为止。
6、用同样的方法,继续求n次算术跟的其它各位上的数(如果已经算了k位数数字,则a要取为全部k位数字)。举例 例如计算987654321987654321的五次算术根,就算到小数点后四位。3 9 7 1. 1 9 2 9 5√987'65432'19876'54321.00000'00000'00000'00000 243________________________________________ 85 41233 19876................................854123319876/(5×390^4)的整数部分是7,用7作试商 83 92970 61757................................397^5-390^5 ___ 1 48262 58119 54321..........................1482625811954321/(5×3970^4)的整数部分是1,用1作试商 1 24265 57094 08851..........................3971^5-3970^5 ___________ 23997 01025 45470 00000....................23997010254547000000/(5×39710^4)的整数部分是1,用1作试商 12433 44352 06091 99551....................39711^5-39710^5_________________________________________ 11563 56673 39378 00449 00000..............1,156,356,673,393,780,044,900,000/(5×397110^4)的整数部分是9,用9作试商 11191 170 21599..............397119^5-397110^5_________________________________________ 372 39671 82334 79932 78401 00000........3723967182334799327840100000/(5×3971190^4)的整数部分是2,用2作试商 248 70419 01386 56554 83574 43232........3971192^5-3971190^5_______________________________________123 69252 80948 23377 94826 56768 00000..123692528094823377948265676800000/(5×39711920^4)的整数部分是9,用9作试商 111 917 71518 74119 30649..39711929^5-39711920^5_______________________________________11 77547 90756 09349 23这样就得到987654321987654321的五次算术根精确到小数点前四位为3971.1929乘方和开方是同级运算! 如果:a^n=b,则 |a|=|b^(1/n)|,不考虑负数的情况: a=b^(1/n)
开方
公式:
例如,开立方,A=5,即k=3.
公式:
开方
开方
5介于
至
之间(1的3次方=1,2的3次方=8)
开方
可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2.0都可以。例如我们取2.0.按照公式:
开方
第一步:
={2.0+[5/(
-2.0]1/3=1.7.}。输入值大于输出值,负反馈;
即5/(2×2)=1.25,1.25-2=-0.75,0.75×1/3=0.25,
2-0.25=1.75,取2位数值,即1.7。
开方
第二步:
={1.7+[5/(
-1.7]1/3=1.71}.。输入值小于输出值,正反馈;
即5/(1.7×1.7)=1.73010,1.73-1.7=0.03,0.03×1/3=0.01,
⒈7+0.01=1.71。取3位数,比前面多取一位数。
开方
第三步:
={1.71+[5/(
-1.71]1/3=1.709}。输入值大于输出值,负反馈
开方
第四步:
={1.709+[5/(
-1.709]1/3=1.7099}.输入值小于输出值,正反馈;
开方
这种方法可以自动调节,第一步与第三步取值偏大,但是计算出来以后输出值会自动转小;第二步,第四步输入值偏小,输出值自动转大。
=1.7099.
 爱华网
爱华网