聚类分析(Cluster Analysis),又称群分析,是根据“物以类聚”的道理,对样品或指标进行分类的一种多元统计分析方法,它们讨论的对象是大量的样品,要求能合理地按各自的特性来进行合理的分类,没有任何模式可供参考或依循,即是在没有先验知识的情况下进行的。聚类源于很多领域,包括数学,计算机科学,统计学,生物学和经济学。将数据分类到不同的类或者簇这样的一个过程,所以同一个簇中的对象有很大的相似性,而不同簇间的对象有很大的相异性。
聚类分析_聚类分析 -定义
依据研究对象(样品或指标)的特征,对其进行分类的方法,减少研究对象的数目。
各类事物缺乏可靠的历史资料,无法确定共有多少类别,目的是将性质相近事物归入一类。
各指标之间具有一定的相关关系。
聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。 聚类分析区别于分类分析(classification analysis) ,后者是有监督的学习。
变量类型:定类变量、定量(离散和连续)变量
聚类方法
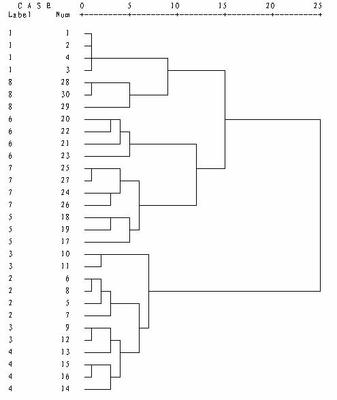
1,层次聚类(Hierarchical Clustering)
合并法、分解法、树状图
2. 非层次聚类
划分聚类、谱聚类
聚类方法特征:
聚类分析简单、直观。
聚类分析主要应用于探索性的研究,其分析的结果可以提供多个可能的解,选择最终的解需要研究者的主观判断和后续的分析;
不管实际数据中是否真正存在不同的类别,利用聚类分析都能得到分成若干类别的解;
聚类分析的解完全依赖于研究者所选择的聚类变量,增加或删除一些变量对最终的解都可能产生实质性的影响。
研究者在使用聚类分析时应特别注意可能影响结果的各个因素。
异常值和特殊的变量对聚类有较大影响
当分类变量的测量尺度不一致时,需要事先做标准化处理。
当然,聚类分析不能做的事情是:
自动发现和告诉你应该分成多少个类――属于非监督类分析方法
期望能很清楚的找到大致相等的类或细分市场是不现实的;
样本聚类,变量之间的关系需要研究者决定;
不会自动给出一个最佳聚类结果;
我这里提到的聚类分析主要是谱系聚类(hierarchical clustering)和快速聚类(K-means)、两阶段聚类(Two-Step);
根据聚类变量得到的描述两个个体间(或变量间)的对应程度或联系紧密程度的度量。
可以用两种方式来测量:
1、采用描述个体对(变量对)之间的接近程度的指标,例如“距离”,“距离”越小的个体(变量)越具有相似性。
2、采用表示相似程度的指标,例如“相关系数”,“相关系数”越大的个体(变量)越具有相似性。
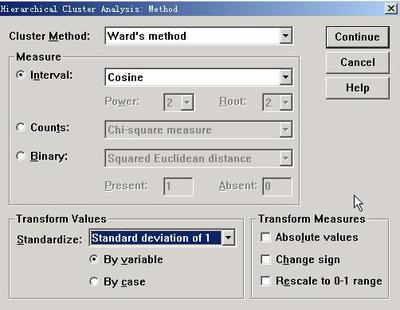
计算聚类――距离指标D(distance)的方法非常多:按照数据的不同性质,可选用不同的距离指标。欧氏距离(Euclidean distance)、欧氏距离的平方(Squared Euclidean distance)、曼哈顿距离(Block)、切比雪夫距离(Chebychev distance)、卡方距离(Chi-Square measure) 等;相似性也有不少,主要是皮尔逊相关系数了!
聚类变量的测量尺度不同,需要事先对变量标准化;
聚类变量中如果有些变量非常相关,意味着这个变量的权重会更大
欧式距离的平方是最常用的距离测量方法;
聚类算法要比距离测量方法对聚类结果影响更大;
标准化方法影响聚类模式:
变量标准化倾向产生基于数量的聚类;
样本标准化倾向产生基于模式的聚类;
一般聚类个数在4-6类,不易太多,或太少;
统计量
群重心
群中心
群间距离
分层步骤
定义问题与选择分类变量
聚类方法
确定群组数目
聚类结果评估
结果的描述、解释
K-means
属于非层次聚类法的一种
(1)执行过程
初始化:选择(或人为指定)某些记录作为凝聚点
循环:
按就近原则将其余记录向凝聚点凝集
计算出各个初始分类的中心位置(均值)
用计算出的中心位置重新进行聚类
如此反复循环,直到凝聚点位置收敛为止
(2)方法特点
通常要求已知类别数
可人为指定初始位置
节省运算时间
样本量大于100时有必要考虑
只能使用连续性变量
过程
特点:
处理对象:分类变量和连续变量
自动决定最佳分类数
快速处理大数据集
前提假设:
变量间彼此独立
分类变量服从多项分布,连续变量服从正态分布
模型稳健
算法原理
第一步:逐个扫描样本,每个样本依据其与已扫描过的样本的距离,被归为以前的类,或生成一个新类
第二步,对第一步中各类依据类间距离进行合并,按一定的标准,停止合并
判别分析 Discriminant Analysis
介绍: 判别分析
分类学是人类认识世界的基础科学。聚类分析和判别分析是研究事物分类的基本方法,广泛地应用于自然科学、社会科学、工农业生产的各个领域。
判别分析DA
概述
DA模型
DA有关的统计量
两组DA
案例分析
判别分析
判别分析是根据表明事物特点的变量值和它们所属的类,求出判别函数。根据判别函数对未知所属类别的事物进行分类的一种分析方法。核心是考察类别之间的差异。
判别分析
不同:判别分析和聚类分析不同的在于判别分析要求已知一系列反映事物特征的数值变量的值,并且已知各个体的分类。
DA适用于定类变量(因)、任意变量(自)
两类:一个判别函数;
多组:一个以上判别函数
DA目的
建立判别函数
检查不同组之间在有关预测变量方面是否有显着差异
决定哪个预测变量对组间差异的贡献最大
根据预测变量对个体进行分类
聚类分析_聚类分析 -判别分析模型
要先建立判别函数 Y=a1x1+a2x2+...anxn,其中:Y为判别分数(判别值),x1 x2...xn为反映研究对象特征的变量,a1 a2...an为系数
聚类分析_聚类分析 -有关统计
典型相关系数
特征值
Wilk's ?(0, 1) = SSw/SSt for X
组重心
分类矩阵
聚类分析_聚类分析 -两组判别
定义问题
估计DA函数系数
确定DA函数的显着性
解释结果
评估有效性
定义问题
判别分析的第一步
第二步就是将样本分为:
分析样本
验证样本
估算判别函数系数
直接法(direct method)就是同时用所有的预测变量估计判别函数,此时每个自变量都包括在内,而不考虑其判别能力。这种方法适用于前期研究或理论模型显示应包括哪些自变量的情况。
逐步判别分析(stepwise discriminant analysis),预测变量依据其对组别的判别能力被逐步引入。
确定显着性
零假设:总体中各组所有判别函数的均值相等。
特征值
典型相关系数
Wilk‘s ?(0, 1) 转换成卡方值检验
见travel.spo
解释结果
系数的符号无关紧要,但能够表示每个变量对判别函数值的影响,以及与特定组的联系。
我们可以通过标准化判别函数系数的绝对值初步判断变量的相对重要性。
通过考察结构相关系数,也可以对预测变量的相对重要性进行判断。
组重心
评估判别分析的有效性
根据分析样本估计出的判别权数,乘以保留样本中的预测变量值,就得出保留样本中每个样本的判别分。
可以根据判别分及适当的规则划分为不同的组别。
命中率(hit ratio)或称样本正确分类概率,就是分类矩阵对角线元素之和与总样本数的比例。
比较样本正确分类百分比与随机正确分类百分比。
聚类分析_聚类分析 -因子分析模型
因子分析模型(FA)
基本思想
因子分析模型
FA的基本思想
“因子分析”于1931年由Thurstone提出,概念起源于Pearson和Spearmen的统计分析
FA用少数几个因子来描述多个变量之间的关系,相关性较高的变量归于同一个因子;
FA利用潜在变量或本质因子(基本特征)去解释可观测变量
FA模型
X1=a11F1+a12F2+ …+a1pFp+v1
X2=a21F1+a22F2+ …+a2pFp+v2 X=AF+V
Xi=ai1F1+ai2F2+ …+aipFp+vi
Xm=ap1F1+ap2F2+ …+ampFm+vm
Xi ― 第i个标准化变量
aip ― 第i个变量对第p个公因子的标准回归系数
F ― 公因子
Vi ― 特殊因子
公因子模型
F1=W11X1+W12X2+ …+W1mXm
F2=W21X1+W22X2+ …+W2mXm
Fi=Wi1X1+Wi2X2+ …+WimXm
Fp=Wp1X1+Wp2X2+ …+WpmXm
Wi ― 权重,因子得分系数
Fi ― 第i个因子的估计值(因子得分)
有关统计量
Bartlett氏球体检验:各变量之间彼此独立
KMO值:FA合适性
因子负荷:相关系数
因子负荷矩阵
公因子方差(共同度)
特征值
方差百分比(方差贡献率)
累计方差贡献率
因子负荷图
碎石图
FA步骤
定义问题
检验FA方法的适用性
确定因子分析方法
因子旋转
解释因子
计算因子得分
注意事项
样本量不能太小
变量相关性
公因子有实际意义
 爱华网
爱华网