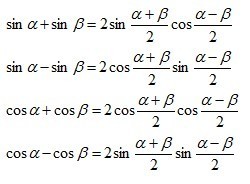又称三角函数的加法定理,是几个角的和(差)的三角函数通过其中各个角的三角函数来表示的关系,包括万能公式,诱导公式等等。
三角函数公式_三角函数和角公式 -诱导公式
常用的诱导公式有以下几组:1.sinα^2 +cosα^2=1
三角函数对应值2.sinα/cosα=tanα
3.tanα=1/cotα
公式一
设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
公式二
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:
sin(π+α)=-sinαcos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三
任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六
π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)
三角函数公式_三角函数和角公式 -一般的最常用公式
口诀;奇变偶不变,符号看象限一般的最常用公式有:
Sin(A+B)=SinA*CosB+SinB*CosA
Sin(A-B)=SinA*CosB-SinB*CosA
Cos(A+B)=CosA*CosB-SinA*SinB
Cos(A-B)=CosA*CosB+SinA*SinB
Tan(A+B)=(TANA+TanB)/(1-TanA*TanB)
Tan(A-B)=(TanA-TanB)/(1+TanA*TanB)
同角三角函数的关系(即同角八式)
平方关系
平方关系:sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
积的关系
积的关系:sinα=tanα*cosα
cosα=cotα*sinα
tanα=sinα*secα
cotα=cosα*cscα
secα=tanα*cscα
cscα=secα*cotα
倒数关系
倒数关系:tanα・cotα=1
sinα・cscα=1
cosα・secα=1
商数关系
商数关系:sina/cosa=tana
cosa/sina=cota
直角三角形ABC中,
角A的正弦值就等于角A的对边比斜边,
sina=y/r
余弦等于角A的邻边比斜边
cosa=x/r
正切等于对边比邻边,
tana=y/x
三角函数恒等变形公式
两角和与差的三角函数
两角和与差的三角函数:
cos(α+β)=cosα・cosβ-sinα・sinβ
cos(α-β)=cosα・cosβ+sinα・sinβsin(α+β)=sinα・cosβ+cosα・sinβ sin(α-β)=sinα・cosβ-cosα・sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα・tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα・tanβ)
辅助角公式
辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
倍角公式
倍角公式:sin(2α)=2sinα・cosα=2/(tanα+cotα)
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
三倍角公式
三倍角公式:sin(3α)=3sinα-4sin^3(α)
cos(3α)=4cos^3(α)-3cosα
半角公式
半角公式:sin(α/2)=±√((1-cosα)/2)
cos(α/2)=±√((1+cosα)/2)
tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα
降幂公式
降幂公式:sin^2(α)=(1-cos(2α))/2=versin(2α)/2
cos^2(α)=(1+cos(2α))/2=vercos(2α)/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
万能公式
万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
积化和差公式
积化和差公式:sinα・cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα・sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα・cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα・sinβ=-(1/2)[cos(α+β)-cos(α-β)]
和差化积公式
和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
其他
其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0
cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及
sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
三角函数公式_三角函数和角公式 -部分高等内容
部分高等内容高等代数中三角函数的指数表示

高等代数中三角函数的指数表示(由泰勒级数易得):
sinx=[e^(ix)-e^(-ix)]/(2i)
cosx=[e^(ix)+e^(-ix)]/2
tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…
此时三角函数定义域已推广至整个复数集。
三角函数作为微分方程的解
三角函数作为微分方程的解:对于微分方程组 y=-y'';y=y'''',有通解Q,可证明
Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。
补充:由相应的指数表示我们可以定义一种类似的函数――双曲函数,其拥有很多与三角函数的类似的性质,二者相映成趣。
三角函数公式_三角函数和角公式 -特殊三角函数值
特殊三角函数值
a 0` 30` 45` 60` 90`sina 0 1/2 √2/2 √3/2 1
cosa 1 √3/2 √2/2 1/2 0
tana 0 √3/3 1 √3 None
cota None √3 1 √3/3 0
15度角的三角函数值:
正弦为(√6-√2)/4;
余弦为(√6+√2)/4;
正切为2-√3,
余切为2+√3。
三角函数公式_三角函数和角公式 -三角函数的计算
三角函数的计算幂级数
c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞)
c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)
它们的各项都是正整数幂的幂函数, 其中c0,c1,c2,...cn...及a都是常数, 这种级数称为幂级数.
泰勒展开式(幂级数展开法):
f(x)=f(a)+f'(a)/1!*(x-a)+f''(a)/2!*(x-a)2+...f(n)(a)/n!*(x-a)n+...
实用幂级数:
ex= 1+x+x2/2!+x3/3!+...+xn/n!+...
ln(1+x)= x-x2/3+x3/3-...(-1)k-1*xk/k+... (|x|<1)
sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<∞)
cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<∞)
arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)
arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)
arctan x = x - x^3/3 + x^5/5 - ... (x≤1)
sinh x = x+x3/3!+x5/5!+...(-1)k-1*x2k-1/(2k-1)!+... (-∞<∞)
cosh x = 1+x2/2!+x4/4!+...(-1)k*x2k/(2k)!+... (-∞<∞)
arcsinh x = x - 1/2*x3/3 + 1*3/(2*4)*x5/5 - ... (|x|<1)
arctanh x = x + x^3/3 + x^5/5 + ... (|x|<1)
--------------------------------------------------------------------------------
三角函数公式_三角函数和角公式 -傅立叶级数
傅立叶级数(三角级数)f(x)=a0/2+∑(n=0..∞) (ancosnx+bnsinnx)
a0=1/π∫(π..-π) (f(x))dx
an=1/π∫(π..-π) (f(x)cosnx)dx
bn=1/π∫(π..-π) (f(x)sinnx)dx
sin2a=2sinacosa
cos2a=cosa^2-sina^2
=1-2sina^2
=2cosa^2-1
tan2a=2tana/1-tana^2
 爱华网
爱华网