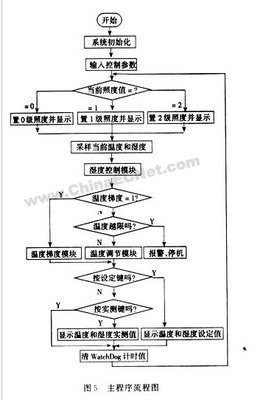
带通滤波器(band-pass filter)是一个允许特定频段的波通过同时屏蔽其他频段的设备,比如RLC振荡回路就是一个模拟带通滤波器。一个理想的带通滤波器应该有一个完全平坦的通带,在通带内没有放大或者衰减,并且在通带之外所有频率都被完全衰减掉,另外,通带外的转换在极小的频率范围完成。除了电子学和信号处理领域之外,带通滤波器应用的一个例子是在大气科学领域,很常见的例子是使用带通滤波器过滤最近3到10天时间范围内的天气数据,这样在数据域中就只保留了作为扰动的气旋。在频带较低的剪切频率f1和较高的剪切频率f2之间是共振频率,这里滤波器的增益最大,滤波器的带宽就是f2和f1之间的差值。
带阻滤波器_带通滤波器 -工作原理
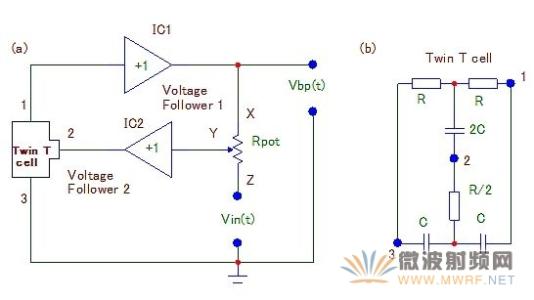
有源带通滤波器电路
一个理想的带通滤波器应该有一个完全平坦的通带,在通带内没有放大或者衰减,
并且在通带之外所有频率都被完全衰减掉,另外,通带外的转换在极小的频率范围完成。
实际上,并不存在理想的带通滤波器。滤波器并不能够将期望频率范围外的所有频率完全衰减掉,尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。这通常称为滤波器的滚降现象,并且使用每十倍频的衰减幅度的dB数来表示。通常,滤波器的设计尽量保证滚降范围越窄越好,这样滤波器的性能就与设计更加接近。然而,随着滚降范围越来越小,通带就变得不再平坦,开始出现“波纹”。这种现象在通带的边缘处尤其明显,这种效应称为吉布斯现象。
除了电子学和信号处理领域之外,带通滤波器应用的一个例子是在大气科学领域,很常见的例子是使用带通滤波器过滤最近3到10天时间范围内的天气数据,这样在数据域中就只保留了作为扰动的气旋。
带通滤波器
在频带较低的剪切频率f1和较高的剪切频率f2之间是共振频率,这里滤波器的增益最大,滤波器的带宽就是f2和f1之间的差值。
带阻滤波器_带通滤波器 -典型应用
许多音响装置的频谱分析器均使用此电路作为带通滤波器,以选出各个不同频段的信号,在显示上利用发光二极管点亮的多少来指示出信号幅度的大小。这种有源带通滤波器的中心频率 ,在中心频率fo处的电压增益Ao=B3/2B1,品质因数 ,3dB带宽B=1/(п*R3*C)也可根据设计确定的Q、fo、Ao值,去求出带通滤波器的各元件参数值。R1=Q/(2пfoAoC),R2=Q/((2Q2-Ao)*2пfoC),R3=2Q/(2пfoC)。上式中,当fo=1KHz时,C取0.01Uf。此电路亦可用于一般的选频放大。
有源带通滤波器电路
此电路亦可使用单电源,只需将运放正输入端偏置在1/2V+并将电阻R2下端接到运放正输入端既可。
带阻滤波器_带通滤波器 -作用
顾名思义,带通滤波器可以理解成为一个电子接口单元,这个单元可以将特定频率范围内的信号传输过去,而阻断这个频率范围以外的信号,达到选择性传输的目的。与此对应,滤波器可以分为低通滤波器,即某频率以下的信号可以传输过去。高通滤波器和带阻滤波器。这些功能都是通过特定电子原件按照不同的布置实现的。比如电容串联可以阻止低频率信号,导通高频率信号。而并联一个电容就可以实现将高频信号短路的功能。又比如电感。串联电感可以导通低频信号,却对高频信号起到阻止的作用。
 爱华网
爱华网