所谓孪生素数指的就是这种间隔为2的相邻素数,它们之间的距离已经近得不能再近了,就象孪生兄弟一样。
孪生素数要介绍孪生素数,首先当然要说一说素数这个概念。素数是除了1和它本身之外没有其它因子的自然数。素数是数论中最纯粹、最令人着迷的概念。除了2之外,所有素数都是奇数(因为否则的话除了1和它本身之外还有一个因子2,从而不满足素数的定义),因此很明显大于2的两个相邻素数之间的最小可能间隔是2。
孪生素数_孪生素数 -简介
孪生素数所谓孪生素数指的就是这种间隔为2的相邻素数,它们之间的距离已经近得不能再近了,就象孪生兄弟一样。最小的孪生素数是(3,5),在100以内的孪生素数还有(5,7),(11,13),(17,19),(29,31),(41,43),(59,61)和(71,73),总计有8组。但是随着数字的增大,孪生素数的分布变得越来越稀疏,寻找孪生素数也变得越来越困难。那么会不会在超过某个界限之后就再也不存在孪生素数了呢?
我们知道,素数本身的分布也是随着数字的增大而越来越稀疏,不过幸运的是早在古希腊时代,Euclid就证明了素数有无穷多个(否则今天许多数论学家就得另谋生路)。长期以来人们猜测孪生素数也有无穷多组,这就是与Goldbach猜想齐名、集令人惊异的简单表述和令人惊异的复杂证明于一身的著名猜想-孪生素数猜想:
孪生素数_孪生素数 -猜想
存在无穷多个素数p,使得p+2也是素数。
究竟谁最早明确提出这一猜想我没有考证过,但是一八四九年法国数学AlphonsedePolignac提出猜想:对于任何偶数2k,存在无穷多组以2k为间隔的素数。对于k=1,这就是孪生素数猜想,因此人们有时把AlphonsedePolignac作为孪生素数猜想的提出者。不同的k对应的素数对的命名也很有趣,k=1我们已经知道叫做孪生素数,k=2(即间隔为4)的素数对被称为cousinprime(比twin远一点),而k=3(即间隔为6)的素数对竟然被称为sexyprime(这回该相信“书中自有颜如玉”了)!不过别想歪了,之所以称为sexyprime其实是因为sex正好是拉丁文中的6。:-)
孪生素数猜想还有一个更强的形式,由英国数学家Hardy和Littlewood于一九二三年提出,现在通常称为Hardy-Littlewood猜想或强孪生素数猜想[注一]。这一猜想不仅提出孪生素数有无穷多组,而且还给出其渐近分布形式为:
x
π2(x)~2C2∫dt/(lnt)^2
2
其中π2(x)表示小于x的孪生素数的数目,C2被称为孪生素数常数(twinprimeconstant),其数值为:
C2=∏P(P-2)/(p-1)^2≈0.66016118158468695739278121100145...
p≥3
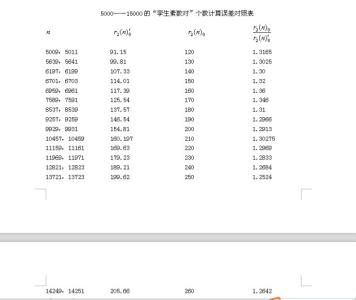
Hardy-Littlewood猜想所给出的孪生素数分布的精确程度可以由下表看出:
x孪生素数数目Hardy-Littlewood猜想
100,00012241249
1,000,0008,1698,248
10,000,00058,98058,754
100,000,000440,312440,368
10,000,000,00027,412,67927,411,417
很明显,Hardy-Littlewood猜想的对孪生素数分布的拟合程度是惊人的。如此精彩的拟合堪与自然科学史上Adams和Leverrier运用天体摄动规律对海王星位置的预言以及Einstein对光线引力偏转的预言相媲美,是理性思维的动人篇章。这种数据对于纯数学的证明虽没有实质的帮助,但是它大大增强了人们对孪生素数猜想的信心。
Hardy-Littlewood猜想所给出的孪生素数分布规律可以通过一个简单的定性分析“得到”:我们知道素数定理(primenumbertheorem)表明对于足够大的x,在x附近素数的分布密度大约为1/ln(x),因此两个素数处于区间2以内的概率大约为2/ln2(x)。这几乎正好就是Hardy-Littlewood猜想中的被积函数!当然其中还差了一个孪生素数常数C2,而这个常数很显然正是Handy与Littlewood的功力深厚之处!
除了Hardy-Littlewood猜想与孪生素数实际分布之间的拟合外,对孪生素数猜想的另一类“实验”支持来自于对越来越大的孪生素数的直接寻找。就象对于大素数的寻找一样,这种寻找在很大程度上成为对计算机运算能力的一种检验,一九九四年十月三十日,这种寻找竟然导致发现了IntelPentium处理器浮点除法运算的一个bug,在工程界引起了不小的震动。截至二零零二年底,人们发现的最大的孪生素数是:
(33218925×2169690-1,33218925×2169690+1)
这对素数中的每一个都长达51090位!许多年来这种记录一直被持续而成功地刷新着。
好了,介绍了这么多关于孪生素数的资料,现在该说说人们在证明孪生素数猜想上所走过的路了。
迄今为止在证明孪生素数猜想上的成果大体可以分为两类。第一类是非估算性的结果,这一方面迄今最好的结果是一九六六年由已故的我国数学家陈景润(顺便说一下,美国数学学会在介绍Goldston和Yildirim成果的简报中提到陈景润时所用的称呼是“伟大的中国数学家陈”)利用筛法(sievemethod)所取得的。陈景润证明了:存在无穷多个素数p,使得p+2要么是素数,要么是两个素数的乘积。这个结果和他关于Goldbach猜想的结果很类似。目前一般认为,由于筛法本身的局限性,这一结果在筛法范围内很难被超越。
证明孪生素数猜想的另一类结果是估算性的,Goldston和Yildirim所取得的结果也属于这一类。这类结果估算的是相邻素数之间的最小间隔,更确切地说是:
Δ:=liminf[(P(n+1)-Pn)/ln(Pn)]
n→∞
翻译成白话文,这个表达式定义的是两个相邻素数之间的间隔与其中较小的那个素数的对数值之比在整个素数集合中所取的最小值。很显然孪生素数猜想如果成立,那么Δ必须等于0,因为孪生素数猜想表明pn+1-pn=2对无穷多个n成立,而ln(pn)→∞,因此两者之比的最小值对于孪生素数集合(从而对于整个素数集合也)趋于零。不过要注意Δ=0只是孪生素数猜想成立的必要条件,而不是充份条件。换句话说如果能证明Δ≠0则孪生素数猜想就不成立,但证明Δ=0却并不意味着孪生素数猜想就一定成立。
对于Δ最简单的估算来自于素数定理。按照素数定理,对于足够大的x,在x附近素数出现的几率为1/ln(x),这表明素数之间的平均间隔为ln(x)(这也正是Δ的表达式中出现ln(pn)的原因),从而(pn+1-pn)/ln(pn)给出的其实是相邻素数之间的间隔与平均间隔的比值,其平均值显然为1。平均值为1,最小值显然是小于等于1,因此素数定理给出Δ≤1。
对Δ的进一步估算始于Hardy和Littlewood。一九二六年,他们运用圆法(circlemethod)证明了假如广义Riemann猜想成立,则Δ≤2/3。这一结果后来被被Rankin改进为Δ≤3/5。但是这两个结果都有赖于本身尚未得到证明的广义Riemann猜想,因此只能算是有条件的结果。一九四零年,Erdös利用筛法首先给出了一个不带条件的结果:Δ<1(即把素数定理给出的结果中的等号部分去掉了)。此后Ricci于一九五五年,Bombieri和Davenport于一九六六年,Huxley于一九七七年,分别把这一结果推进到Δ≤15/16,Δ≤(2+√3)/8≈0.4665及Δ≤0.4425。Goldston和Yildirim之前最好的结果是Maier在一九八六年取得的Δ≤0.2486。
以上这些结果都是在小数点后做文章,Goldston和Yildirim的结果把这一系列的努力大大推进了一步,并且-如果得到证实的话-将在一定意义上终结对Δ进行数值估算的长达几十年的征途,因为Goldston和Yildirim证明了Δ=0。当然如我们前面所说,Δ=0只是孪生素数猜想成立的必要条件,而非充份条件,因此Goldston和Yildirim的结果离最终证明孪生素数猜想还远得很,但它无疑是近十几年来这一领域中最引人注目的结果。
一旦Δ=0被证明,人们的注意力自然就转到了研究Δ趋于0的方式上来。孪生素数猜想要求Δ~[log(pn)]-1(因为pn+1-pn=2对无穷多个n成立)。Goldston和Yildirim的证明给出的是Δ~[log(pn)]-1/9,两者之间还有相当距离。但是看过Goldston和Yildirim手稿的一些数学家认为Goldston和Yildirim所用的方法明显存在改进的空间,也就是说对Δ趋于0的方式可以给出更强的估计。因此Goldston和Yildirim的证明其价值不仅仅在于结果本身,更在于它很有可能成为未来一系列研究的起点。这种系列研究对于数学来说有着双重的价值,因为一方面这种研究所获得的新结果是对数学的直接贡献,另一方面这种研究对Goldston和Yildirim的证明会起到反复推敲和核实的作用。现代数学早已超越了一两个评审花一两个小时就可以对一个数学证明做出评判的时代。以前四色定理和Fermat大定理都曾有过一个证明时隔几年(甚至十几年)才被发现错误的例子。因此一个复杂的数学结果能够成为进一步研究的起点,吸引其它数学家的参与对于最终判定该结果的正确性具有极其正面的意义。
注释:
[注一]Hardy-Littlewood于一九二三年提出的猜想共有两个,其中第一个猜想又称为k-tuple猜想,它给出了所有形如(p,p+2m1,...,p+2mk)(其中0<m1<...<mk)的素数k-tuple的渐进分布。强孪生素数猜想只是t-tuple猜想的一部分。
孪生素数_孪生素数 -简易证明
大于3的素数存在于等差数列6N+1和6N+5之中。所谓孪生素数,即相差为2的两个素数叫孪生素数。即当6N+5的N为X,6N+1的N为X+1时,6X+5和6(X+1)+1都是素数时,即为孪生素数。又因为,人们已经证明了素数永远存在,那么,当6X+5和6(X+1)+1都是素数也永远存在,所以,孪生素数永远存在。
设所取的范围为M,当所取的范围≥13时,范围内的孪生素数组个数≥K(√M)/2。
式中的K=(9/7)*(15/13)*(21/19)*(25/23)*(27/25)*……*Y/(Y-2),Y为√M内的最大奇合数。
相差4的孪生素数。也就是6N+1和6N+5所形成的孪生素数。这里的6N+1中的N与6N+5中的N相等时,6N+1和6N+5都是素数,叫做相差4的孪生素数。同理,人们已经证明了素数永远存在,所以,6N+1和6N+5都是素数也永远存在,应该以上面的孪生素数个数相当。
相差6的孪生素数,即6N+1与6(N+1)+1,6N+5与(6N+1)+5。为相同等差数列所形成的孪生素数。同理,人们已经证明了素数永远存在,所以,6N+1与6(N+1)+1,6N+5与(6N+1)+5都是素数也永远存在,应该有相差2的孪生素数个数的两倍。
孪生素数的直接寻找方法,敬请搜索《孪生素数的计算及证明》。该筛选方法,除了孪生素数3,5以外,不会漏掉任何一个孪生素数。因为,本文认为:孪生素数的起源是孪生素数5,7。后面所有的孪生素数都是孪生素数5,7的延伸。
虽然不能证明孪生素数有无穷多对,但可以帮助数学爱好者证明:素数除了2以外都是奇数,而奇数除了(奇数*奇数)(或再加“*奇数”)以外都是素数,那么孪生素数有有限对的等价就是超出一个范围后每隔4或2就有一个是n个奇数的乘积。
补充:壹
作者:王敏
一。三个奇孪生素数对只有3,5,7
证明;∵> 7 的三个奇素数对必能被六整除
二。对于相差为2的孪生素数有以下几种分布:
(一)存在6N±1的奇孪生素数对,以下为1500以内的奇孪生素数对的分布状况:
当N =1,2,3,5,7,10,12,17,18,23,25,30,32,33,76,40,45,47,52,58,70,72,77,87,95,100,103,107,110,135,137,138,143,147,170,172,175,177,182,192,205,213,215,217,220,238,242,247,248,....
除n=1是三连珠以外,从中发现个位数中没有1,4,9.
(二)在n2+n的地方存在±1的素数对:例如在22加2=6的地方有孪生素数5,7。.还有n=2,3,5,6,8,15,21,24,。。。
(三)在有的n2区间内无孪生素数对:例如在92与102之间没有孪生数。集体有当n=9,19,26,27,30,34,...
三。几种相差大于2的孪生素数分布情况;
(一)相差为4的孪生素数:存在(3×奇数n)±2的分布特点:
n=3,5,7,13,15,23,43,55,65,75,77,93,....
据此观察,个位数为3,5,7.
(二)相差为6的孪生素数:存在2n±3 (3├ n) 的孪生素数:
n = 13,17,28,32,38,43,67,85,88,118,127,130,133,137,...
据此观察,个位数中无1,4.,6,9.
注“├”表示不能整除。
补充完
孪生素数_孪生素数 -相关词条
费马大定理黎曼假设四色原理哥德巴赫猜想常量
孪生素数_孪生素数 -参考资料
http://www.changhai.org/contents/science/mathematics/twin_prime.html
 爱华网
爱华网



