本书是为理工科大学各专业普遍开设的“数值分析”课程编写的教材。其内容包括插值与逼近,数值微分与数值积分,非线性方程与线性方程组的数值解法,矩阵的特征值与特征向量计算,常微分方程数值解法。每章附有习题并在书末给出了部分答案,每章还附有复习与思考题和计算实习题。全书阐述严谨,脉络分明,深入浅出,便于教学。本书也可作为理工科大学各专业研究生学位课程的教材,并可供从事科学计算的科技工作者参考。
数值分析_数值分析 -前言
本书第5版已列入普通高等教育“十一五”国家级规划教材,主要作为理科数学类专业本科生及其他理工科硕士研究生“数值分析”课程的教材. 根据“数值分析”课程教学大纲的要求,对第4版做了适当修改,但仍保留原教材的基本结构和大部分内容. 主要修改部分如下:
(1) 在内容上精简了一些较少使用的算法及一些较繁杂的推导和证明;加强了算法基本思想的分析和使用的说明;另外还增加了一些新内容,如自适应求积和重积分的计算,解线性方程组的共轭梯度法,代数方程求根的病态分析,常微分方程数值解法中多步法的收敛性与稳定性分析,刚性问题等.
(2) 评注中增加了一些历史发展及使用数学软件的说明;每章增加了复习与思考题,这有助于读者加深对基本内容的理解,促进对所讲算法的掌握;另外为加强使用计算机解题练习,增添了一些计算实习题.
(3) 根据本书新版的特点,删去了并行算法的附录,有关并行算法目前有很多普及的入门着作,需要了解的可自己学习. 另外,本书推荐读者使用MATLAB语言及数学库,有关MATLAB的使用本书也不做介绍,目前也有很多介绍的书籍可供参考.
本书第5版主要由李庆扬负责修改,是在清华大学出版社及本书编辑刘颖博士推动和支持下完成的,还得到清华大学给予的经费资助,作者对他们的支持和帮助表示衷心感谢.
希望使用本书的老师和同学对本书存在的问题给予批评指正.
作 者
2008年元旦
数值分析_数值分析 -目录
第1章 数值分析与科学计算引论(1(指第一页))
1.1 数值分析的对象、作用与特点(1)
1.1.1 数学科学与数值分析(1)
1.1.2 计算数学与科学计算(1)
1.1.3 计算方法与计算机(2)
1.1.4 数值问题与算法(2)
1.2 数值计算的误差(3)
1.2.1 误差来源与分类(3)
1.2.2 误差与有效数字(4)
1.2.3 数值运算的误差估计(7)
1.3 误差定性分析与避免误差危害(8)
1.3.1 算法的数值稳定性(9)
1.3.2 病态问题与条件数(10)
1.3.3 避免误差危害(11)
1.4 数值计算中算法设计的技术(13)
1.4.1 多项式求值的秦九韶算法(13)
1.4.2 迭代法与开方求值(14)
1.4.3 以直代曲与化整为"零"(15)
1.4.4 加权平均的松弛技术(16)
1.5 数学软件(17)
评注(18)
复习与思考题(19)
习题(19)
第2章 插值法(22)
2.1 引言(22)
2.1.1 插值问题的提出(22)
2.1.2 多项式插值(23)
2.2 拉格朗日插值(23)
2.2.1 线性插值与抛物线插值(23)
2.2.2 拉格朗日插值多项式(25)
2.2.3 插值余项与误差估计(26)
2.3 均差与牛顿插值多项式(29)
2.3.1 插值多项式的逐次生成(29)
2.3.2 均差及其性质(30)
2.3.3 牛顿插值多项式(31)
2.3.4 差分形式的牛顿插值公式(32)
2.4 埃尔米特插值(35)
2.4.1 重节点均差与泰勒插值(35)
2.4.2 两个典型的埃尔米特插值(36)
2.5 分段低次插值(39)
2.5.1 高次插值的病态性质(39)
2.5.2 分段线性插值(40)
2.5.3 分段三次埃尔米特插值(40)
2.6 三次样条插值(41)
2.6.1 三次样条函数(41)
2.6.2 样条插值函数的建立(42)
2.6.3 误差界与收敛性(46)
评注(46)
复习与思考题(47)
习题(48)
计算实习题(50)
第3章 函数逼近与快速傅里叶变换(51)
3.1 函数逼近的基本概念(51)
3.1.1 函数逼近与函数空间(51)
3.1.2 范数与赋范线性空间(52)
3.1.3 内积与内积空间(53)
3.1.4 最佳逼近(56)
3.2 正交多项式(57)
3.2.1 正交函数族与正交多项式(57)
3.2.2 勒让德多项式(59)
3.2.3 切比雪夫多项式(61)
3.2.4 切比雪夫多项式零点插值(63)
3.2.5 其他常用的正交多项式(65)
3.3 最佳平方逼近(67)
3.3.1 最佳平方逼近及其计算(67)
3.3.2 用正交函数族作最佳平方逼近(69)
3.3.3 切比雪夫级数(72)
3.4 曲线拟合的最小二乘法(73)
3.4.1 最小二乘法及其计算(73)
3.4.2 用正交多项式作最小二乘拟合(76)
3.5 有理逼近(78)
3.5.1 有理逼近与连分式(78)
3.5.2 帕德逼近(80)
3.6 三角多项式逼近与快速傅里叶变换(83)
3.6.1 最佳平方三角逼近与三角插值(84)
3.6.2 N点DFT与FFT算法(86)
评注(92)
复习与思考题(92)
习题(94)
计算实习题(95)
第4章 数值积分与数值微分(97)
4.1 数值积分概论(97)
4.1.1 数值积分的基本思想(97)
4.1.2 代数精度的概念(98)
4.1.3 插值型的求积公式(100)
4.1.4 求积公式的余项(101)
4.1.5 求积公式的收敛性与稳定性(102)
4.2 牛顿-柯特斯公式(103)
4.2.1 柯特斯系数与辛普森公式(103)
4.2.2 偶阶求积公式的代数精度(105)
4.2.3 辛普森公式的余项(105)
4.3 复合求积公式(106)
4.3.1 复合梯形公式(106)
4.3.2 复合辛普森求积公式(107)
4.4 龙贝格求积公式(109)
4.4.1 梯形法的递推化(109)
4.4.2 外推技巧(110)
4.4.3 龙贝格算法(112)
4.5 自适应积分方法(113)
4.6 高斯求积公式(116)
4.6.1 一般理论(116)
4.6.2 高斯-勒让德求积公式(121)
4.6.3 高斯-切比雪夫求积公式(123)
4.6.4 无穷区间的高斯型求积公式(124)
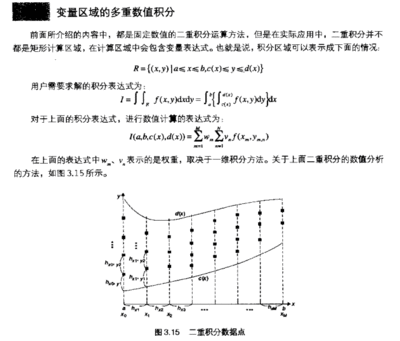
4.7 多重积分(126)
4.8 数值微分(128)
4.8.1 中点方法与误差分析(128)
4.8.2 插值型的求导公式(130)
4.8.3 三次样条求导(132)
4.8.4 数值微分的外推算法(132)
评注(133)
复习与思考题(134)
习题(135)
计算实习题(137)
第5章 解线性方程组的直接方法(138)
5.1 引言与预备知识(138)
5.1.1 引言(138)
5.1.2 向量和矩阵(138)
5.1.3 矩阵的特征值与谱半径(139)
5.1.4 特殊矩阵(141)
5.2 高斯消去法(142)
5.2.1 高斯消去法(142)
5.2.2 矩阵的三角分解(146)
5.2.3 列主元消去法(148)
5.3 矩阵三角分解法(152)
5.3.1 直接三角分解法(152)
5.3.2 平方根法(156)
5.3.3 追赶法(159)
5.4 向量和矩阵的范数(161)
5.4.1 向量范数(161)
5.4.2 矩阵范数(164)
5.5 误差分析(167)
5.5.1 矩阵的条件数(167)
5.5.2 迭代改善法(172)
评注(174)
复习与思考题(174)
习题(175)
计算实习题(178)
第6章 解线性方程组的迭代法(180)
6.1 迭代法的基本概念(180)
6.1.1 引言(180)
6.1.2 向量序列与矩阵序列的极限(182)
6.1.3 迭代法及其收敛性(183)
6.2 雅可比迭代法与高斯-塞德尔迭代法(187)
6.2.1 雅可比迭代法(187)
6.2.2 高斯-塞德尔迭代法(188)
6.2.3 雅可比迭代与高斯-塞德尔迭代收敛性(190)
6.3 超松弛迭代法(193)
6.3.1 逐次超松弛迭代法(193)
6.3.2 SOR迭代法的收敛性(195)
6.3.3 块迭代法(197)
6.4 共轭梯度法(202)
6.4.1 与方程组等价的变分问题(202)
6.4.2 最速下降法(203)
6.4.3 共轭梯度法(CG方法)(204)
评注(208)
复习与思考题(208)
习题(209)
计算实习题(211)
第7章 非线性方程与方程组的数值解法(212)
7.1 方程求根与二分法(212)
7.1.1 引言(212)
7.1.2 二分法(213)
7.2 不动点迭代法及其收敛性(215)

7.2.1 不动点与不动点迭代法(215)
7.2.2 不动点的存在性与迭代法的收敛性(216)
7.2.3 局部收敛性与收敛阶(218)
7.3 迭代收敛的加速方法(220)
7.3.1 埃特金加速收敛方法(220)
7.3.2 斯特芬森迭代法(221)
7.4 牛顿法(222)
7.4.1 牛顿法及其收敛性(222)
7.4.2 牛顿法应用举例(224)
7.4.3 简化牛顿法与牛顿下山法(225)
7.4.4 重根情形(226)
7.5 弦截法与抛物线法(228)
7.5.1 弦截法(228)
7.5.2 抛物线法(229)
7.6 求根问题的敏感性与多项式的零点(230)
7.6.1 求根问题的敏感性与病态代数方程(230)
7.6.2 多项式的零点(232)
7.7 非线性方程组的数值解法(233)
7.7.1 非线性方程组(233)
7.7.2 多变量方程的不动点迭代法(234)
7.7.3 非线性方程组的牛顿迭代法(236)
评注(236)
复习与思考题(237)
习题(238)
计算实习题(239)
第8章 矩阵特征值计算(241)
8.1 特征值性质和估计(241)
8.1.1 特征值问题及其性质(241)
8.1.2 特征值估计与扰动(242)
8.2 幂法及反幂法(245)
8.2.1 幂法(245)
8.2.2 加速方法(248)
8.2.3 反幂法(251)
8.3 正交变换与矩阵分解(254)
8.3.1 豪斯霍尔德变换(254)
8.3.2 吉文斯变换(256)
8.3.3 矩阵的QR分解与舒尔分解(258)
8.3.4 用正交相似变换约化一般矩阵为上海森柏格矩阵(261)
8.4 QR方法(264)
8.4.1 QR算法(264)
8.4.2 带原点位移的QR方法(266)
8.4.3 用单步QR方法计算上海森伯格矩阵的特征值(268)
8.4.4 双步QR方法(隐式QR方法)(272)
评注(274)
复习与思考题(274)
习题(275)
计算实习题(277)
第9章 常微分方程初值问题数值解法(279)
9.1 引言(279)
9.2 简单的数值方法(280)
9.2.1 欧拉法与后退欧拉法(280)
9.2.2 梯形方法(282)
9.2.3 改进欧拉公式(283)
9.2.4 单步法的局部截断误差与阶(284)
9.3 龙格-库塔方法(286)
9.3.1 显式龙格-库塔法的一般形式(286)
9.3.2 二阶显式R-K方法(287)
9.3.3 三阶与四阶显式R-K方法(288)
9.3.4 变步长的龙格-库塔方法(290)
9.4 单步法的收敛性与稳定性(291)
9.4.1 收敛性与相容性(291)
9.4.2 绝对稳定性与绝对稳定域(293)
9.5 线性多步法(297)
9.5.1 线性多步法的一般公式(297)
9.5.2 阿当姆斯显式与隐式公式(299)
9.5.3 米尔尼方法与辛普森方法(301)
9.5.4 汉明方法(302)
9.5.5 预测-校正方法(303)
9.5.6 构造多步法公式的注记和例(305)
9.6 线性多步法的收敛性与稳定性(306)
9.6.1 相容性及收敛性(307)
9.6.2 稳定性与绝对稳定性(308)
9.7 一阶方程组与刚性方程组(310)
9.7.1 一阶方程组(310)
9.7.2 化高阶方程为一阶方程组(312)
9.7.3 刚性方程组(313)
评注(315)
复习与思考题(315)
习题(316)
计算实习题(318)
部分习题答案(320)
参考文献(325)
 爱华网
爱华网