协方差分析是建立在方差分析和回归分析基础之上的一种统计分析方法。方差分析是从质量因子的角度探讨因素不同水平对实验指标影响的差异。一般说来,质量因子是可以人为控制的。回归分析是从数量因子的角度出发,通过建立回归方程来研究实验指标与一个(或几个)因子之间的数量关系。但大多数情况下,数量因子是不可以人为加以控制的。两个不同参数之间的方差就是协方差。若两个随机变量X和Y相互独立,则E[(X-E(X))(Y-E(Y))]=0,因而若上述数学期望不为零,则X和Y必不是相互独立的,亦即它们之间存在着一定的关系。
协方差_协方差 -?百科名片
协方差
协方差分析是建立在方差分析和回归分析基础之上的一种统计分析方法。 方差分析是从质量因子的角度探讨因素不同水平对实验指标影响的差异。一般说来,质量因子是可以人为控制的。 回归分析是从数量因子的角度出发,通过建立回归方程来研究实验指标与一个(或几个)因子之间的数量关系。但大多数情况下,数量因子是不可以人为加以控制的。
协方差_协方差 -属性
两个不同参数之间的方差就是协方差 若两个随机变量X和Y相互独立,则E[(X-E(X))(Y-E(Y))]=0,因而若上述数学期望不为零,则X和Y必不是相互独立的,亦即它们之间存在着一定的关系。
定义
E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差,记作Cov(X,Y),即Cov(X,Y)=E[(X-E(X))(Y-E(Y))]。
协方差与方差之间有如下关系:
D(X+Y)=D(X)+D(Y)+2Cov(X,Y)
D(X-Y)=D(X)+D(Y)-2Cov(X,Y)
协方差与期望值有如下关系:
Cov(X,Y)=E(XY)-E(X)E(Y)。
协方差的性质:
(1)Cov(X,Y)=Cov(Y,X);
(2)Cov(aX,bY)=abCov(X,Y),(a,b是常数);
(3)Cov(X+X,Y)=Cov(X,Y)+Cov(X,Y)。
由协方差定义,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。
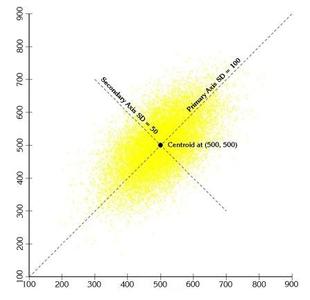
协方差作为描述X和Y相关程度的量,在同一物理量纲之下有一定的作用,但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念:
协方差
定义
称为随机变量X和Y的(Pearson)相关系数。
定义
若ρXY=0,则称X与Y不线性相关。
即ρXY=0的充分必要条件是Cov(X,Y)=0,亦即不相关和协方差为零是等价的。
定理
设ρXY是随机变量X和Y的相关系数,则有
(1)
 爱华网
爱华网