在数学中,两个集合X和Y的笛卡儿积(Cartesian product),又称直积,表示为X × Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员。假设集合A=a, b,集合B=0, 1, 2,则两个集合的笛卡尔积为(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)。类似的例子有,如果A表示某学校学生的集合,B表示该学校所有课程的集合,则A与B的笛卡尔积表示所有可能的选课情况。A表示所有声母的集合,B表示所有韵母的集合,那么A和B的笛卡尔积就为所有可能的汉字全拼。
笛卡尔乘积_笛卡尔乘积 -定义
笛卡尔乘积
设A,B为集合,用A中元素为第一元素,B中元素为第二元素构成有序对,所有这样的有序对组成的集合叫做A与B的笛卡尔积,记作AxB.
笛卡尔积的符号化为:
A×B={(x,y)|x∈A∧y∈B}
例如,A={a,b}, B={0,1,2},则
A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}
笛卡尔乘积_笛卡尔乘积 -运算性质
1.对任意集合A,根据定义有
AxΦ =Φ ,Φ xA=Φ
2.一般地说,笛卡尔积运算不满足交换律,即
AxB≠BxA(当A≠Φ ∧B≠Φ∧A≠B时)
3.笛卡尔积运算不满足结合律,即
(AxB)xC≠Ax(BxC)(当A≠Φ ∧B≠Φ∧C≠Φ时)
4.笛卡尔积运算对并和交运算满足分配律,即
Ax(B∪C)=(AxB)∪(AxC)
(B∪C)xA=(BxA)∪(CxA)
Ax(B∩C)=(AxB)∩(AxC)
(B∩C)xA=(BxA)∩(CxA)
笛卡尔乘积_笛卡尔乘积 -相关案例
给出三个域:
D1=SUPERVISOR ={ 张清玫,刘逸 }
D2=SPECIALITY={计算机专业,信息专业}
D3=POSTGRADUATE={李勇,刘晨,王敏}
则D1,D2,D3的笛卡尔积为D:
D=D1×D2×D3 =
{(张清玫,计算机专业,李勇),(张清玫,计算机专业,刘晨),
(张清玫,计算机专业,王敏),(张清玫,信息专业,李勇),
(张清玫,信息专业,刘晨),(张清玫,信息专业,王敏),
(刘逸,计算机专业,李勇),(刘逸,计算机专业,刘晨),
(刘逸,计算机专业,王敏),(刘逸,信息专业,李勇),
(刘逸,信息专业,刘晨),(刘逸,信息专业,王敏) }
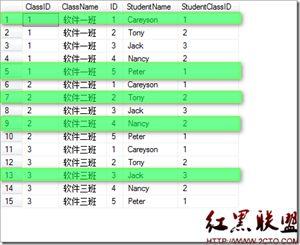
这样就把D1,D2,D3这三个集合中的每个元素加以对应组合,形成庞大的集合群。
本个例子中的D中就会有2X2X3个元素,如果一个集合有1000个元素,有这样3个集合,他们的笛卡尔积所组成的新集合会达到十亿个元素。假若某个集合是无限集,那么新的集合就将是有无限个元素。
笛卡尔乘积_笛卡尔乘积 -程序代码
C#源代码
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
using System.Linq;
public class Descartes
{
public static void run(List>dimvalue, Listresult, int layer, string curstring)
{
if (layer
{
if (dimvalue[layer].Count == 0)
run(dimvalue, result, layer + 1, curstring);
else
{
for (int i = 0; i
{
StringBuilder s1 = new StringBuilder();
s1.Append(curstring);
s1.Append(dimvalue[layer][i]);
run(dimvalue, result, layer + 1, s1.ToString());
}
}
}
else if (layer == dimvalue.Count - 1)
{
if (dimvalue[layer].Count == 0) result.Add(curstring);
else
{
for (int i = 0; i
{
result.Add(curstring + dimvalue[layer][i]);
}
}
}
}
}
程序使用说明
(1)将每个维度的集合的元素视为List,多个集合构成List>dimvalue作为输入
(2)将多维笛卡尔乘积的结果放到Listresult之中作为输出
(3)int layer, string curstring只是两个中间过程的参数携带变量
(4)程序采用递归调用,起始调用示例如下:
Listresult = new List();
Descartes.run(dimvalue, result, 0, "");
即可获得多维笛卡尔乘积的结果。
 爱华网
爱华网