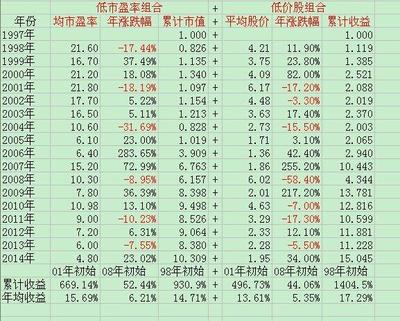
投资组合理论(Portfolio Theory),是指若干种证券组成的投资组合,其收益是这些证券收益的加权平均数,但是其风险不是这些证券风险的加权平均风险,投资组合能降低非系统性风险。美国经济学家马考维茨(Markowitz)于1952年首次提出投资组合理论,并进行了系统、深入和卓有成效的研究,他因此获得了诺贝尔经济学奖。
投资组合理论_投资组合理论 -内容
该理论包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
在发达的证券市场中,马科维茨投资组合理论早已在实践中被证明是行之有效的,并且被广泛应用于组合选择和资产配置。但是,我国的证券理论界和实务界对于该理论是否适合于我国股票市场一直存有较大争议。
从狭义的角度来说,投资组合是规定了投资比例的一揽子有价证券,当然,单只证券也可以当作特殊的投资组合。本文讨论的投资组合限于由股票和无风险资产构成的投资组合。
人们进行投资,本质上是在不确定性的收益和风险中进行选择。投资组合理论用均值―方差来刻画这两个关键因素。所谓均值,是指投资组合的期望收益率,它是单只证券的期望收益率的加权平均,权重为相应的投资比例。当然,股票的收益包括分红派息和资本增值两部分。所谓方差,是指投资组合的收益率的方差。我们把收益率的标准差称为波动率,它刻画了投资组合的风险。
人们在证券投资决策中应该怎样选择收益和风险的组合呢?这正是投资组合理论研究的中心问题。投资组合理论研究“理性投资者”如何选择优化投资组合。所谓理性投资者,是指这样的投资者:他们在给定期望风险水平下对期望收益进行最大化,或者在给定期望收益水平下对期望风险进行最小化。
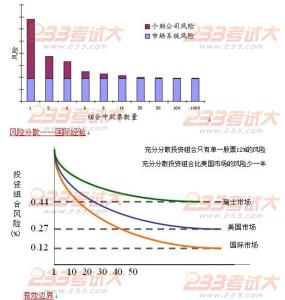
因此把上述优化投资组合在以波动率为横坐标,收益率为纵坐标的二维平面中描绘出来,形成一条曲线。这条曲线上有一个点,其波动率最低,称之为最小方差点(英文缩写是MVP)。这条曲线在最小方差点以上的部分就是著名的(马考维茨)投资组合有效边界,对应的投资组合称为有效投资组合。投资组合有效边界一条单调递增的凹曲线。
投资组合理论
如果投资范围中不包含无风险资产(无风险资产的波动率为零),曲线AMB是一条典型的有效边界。A点对应于投资范围中收益率最高的证券。
如果在投资范围中加入无风险资产,那么投资组合有效边界是曲线AMC。C点表示无风险资产,线段CM是曲线AMB的切线,M是切点。M点对应的投资组合被称为“市场组合”。
如果市场允许卖空,那么AMB是二次曲线;如果限制卖空,那么AMB是分段二次曲线。在实际应用中,限制卖空的投资组合有效边界要比允许卖空的情形复杂得多,计算量也要大得多。
在波动率-收益率二维平面上,任意一个投资组合要么落在有效边界上,要么处于有效边界之下。因此,有效边界包含了全部(帕雷托)最优投资组合,理性投资者只需在有效边界上选择投资组合。
投资组合理论_投资组合理论 -产生发展
现代投资组合理论主要由投资组合理论、资本资产定价模型、APT模型、有效市场理论以及行为金融理论等部分组成。它们的发展极大地改变了过去主要依赖基本分析的传统投资管理实践,使现代投资管理日益朝着系统化、科学化、组合化的方向发展。
1952年3月,美国经济学哈里・马考威茨发表了《证券组合选择》的论文,作为现代证券组合管理理论的开端。马克威茨对风险和收益进行了量化,建立的是均值方差模型,提出了确定最佳资产组合的基本模型。由于这一方法要求计算所有资产的协方差矩阵,严重制约了其在实践中的应用。
1963年,威廉・夏普提出了可以对协方差矩阵加以简化估计的单因素模型,极大地推动了投资组合理论的实际应用。
20世纪60年代,夏普、林特和莫森分别于1964、1965和1966年提出了资本资产定价模型(CAPM)。该模型不仅提供了评价收益一风险相互转换特征的可运作框架,也为投资组合分析、基金绩效评价提供了重要的理论基础。
1976年,针对CAPM模型所存在的不可检验性的缺陷,罗斯提出了一种替代性的资本资产定价模型,即APT模型。该模型直接导致了多指数投资组合分析方法在投资实践上的广泛应用。
投资组合理论_投资组合理论 -其他论述
(portfolio theory)
投资组合理论风险管理的数量分析。
投资组合理论被定义为最佳风险管理的定量分析。无论分析的单位是家庭、公司,还是其他经济组织,为了找到最优的行动方案,需要在减少风险的成本与收益之间进行权衡,对这些内容阐述并估计的过程,即投资组合理论的应用。
对家庭而言,消费和风险偏好是已知的。偏好会随着时间而改变,但这些变化的机制和原因并非投资组合理论阐述的内容。投资组合理论阐述了如何在金融工具中进行选择,以使其特定的偏好最大化。通常,最佳选择包括对获取较高预期回报和承担较大风险之间权衡的评估。
投资组合理论_投资组合理论 -应用问题
马考威茨的投资组合理论不但为分散投资提供了理论依据,而且也为如何进行有效的分散投资提供了分析框架。但在实际运用中,马考威茨模型也存在着一定的局限性和困难:
1.马考威茨模型所需要的基本输入包括证券的期望收益率、方差和两两证券之间的协方差。当证券的数量较多时,基本输入所要求的估计量非常大,从而也就使得马考威茨的运用受到很大限制。因此,马考威茨模型目前主要被用在资产配置的最优决策上。
2.数据误差带来的解的不可靠性。马考威茨模型需要将证券的期望收益率、期望的标准差和证券之间的期望相关系数作为已知数据作为基本输入。如果这些数据 没有估计误差,马考威茨模型就能够保证得到有效的证券组合。但由于期望数据是未知的,需要进行统计估计,因此这些数据就不会没有误差。这种由于统计估计而带来的数据输入方面的不准确性会使一些资产类别的投资比例过高而使另一些资产类别的投资比例过低。
3.解的不稳定性。马考威茨模型的另一个应用问题是输人数据的微小改变会导致资产权重的很大变化。解的不稳定性限制了马考威茨模型在实际制定资产配置政策方面的应用。如果基于季度对输人数据进行重新估计,用马考威茨模型就会得到新的资产权重的解,新的资产权重与上一季度的权重差异可能很大。这意味着必须对资产组合进行较大的调整,而频繁的调整会使人们对马考威茨模型产生不信任感。
4.重新配置的高成本。资产比例的调整会造成不必要的交易成本的上升。资产比例的调整会带来很多不利的影响,因此正确的政策可能是维持现状而不是最优化。
 爱华网
爱华网