机器的主体部分由许多运动构件组成,用于传递运动和力。由一个构件为机架的、构件间能够相对运动的构件系统称为机构。所有构件都在相互平行的平面内运动的机构称为平面机构。平面连杆机构运动设计的方法主要是几何法和解析法,此外还有图谱法和模型实验法。平面连杆机构中最常用的是四杆机构,它的构件数目最少,且能转换运动。几何法是利用机构运动过程中各运动副位置之间的几何关系,通过作图获得有关运动尺寸,所以几何法直观形象,几何关系清晰,对于一些简单设计问题的处理是有效而快捷的,但由于作图误差的存在,所以设计精度较低。
连杆机构_平面连杆机构 -简介
低副是面接触,耐磨损;加上转动副和移动副的接触表面是圆柱面和平面,制造简便,易于获得较高的制造精度。因此,平面连杆机构在各种机械和仪器中获得广泛应用。连杆机构的缺点是:低副中存在间隙,数目较多的低副会引起运动累积误差;而且它的设计比较复杂,不易精确地实现复杂地运动规律。
最简单地平面连杆机构是由四个构建组成地,称为平面四杆机构。它的应用非常广泛,而且是组成多杆机构的基础。
平面连杆机构
由若干个刚性构件通过低副(转动副、移动副)联接,且各构件上各点的运动平面均相互
平行的机构(图1),又称平面低副机构。低副具有压强小、磨损轻、易于加工和几何形状能保证本身封闭等优点,故平面连杆机构广泛用于各种机械和仪器中。与高副机构相比,它难以准确实现预期运动,设计计算复杂。
平面连杆机构中最常用的是四杆机构,它的构件数目最少,且能转换运动。多于四杆的平面连杆机构称多杆机构,它能实现一些复杂的运动,但杆多且稳定性差。
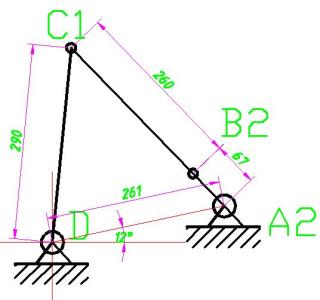
连杆机构_平面连杆机构 -基本问题
平面连杆机构的运动设计一般可归纳为以下三类基本问题:
1) 实现构件给定位置(亦称刚体导引),即要求连杆机构能引导某构件按规定顺序精确或近似地经过给定的若干位置。
2) 实现已知运动规律(亦称函数生成),即要求主、从动件满足已知的若干组对应位置关系,包括满足一定的急回特性要求,或者在主动件运动规律一定时,从动件能精确或近似地按给定规律运动。
3) 实现已知运动轨迹(亦称轨迹生成),即要求连杆机构中作平面运动的构件上某一点精确或近似地沿着给定的轨迹运动。
在进行平面连杆机构运动设计时,往往是以上述运动要求为主要设计目标,同时还要兼顾一些运动特性和传力特性等方面的要求,如整转副要求、压力角或传动角要求、机构占据空间位置要求等。另外,设计结果还应满足运动连续性要求,即当主动件连续运动时,从动件也能连续地占据预定的各个位置,而不能出现错位或错序等现象。
平面连杆机构运动设计的方法主要是几何法和解析法,此外还有图谱法和模型实验法。几何法是利用机构运动过程中各运动副位置之间的几何关系,通过作图获得有关运动尺寸,所以几何法直观形象,几何关系清晰,对于一些简单设计问题的处理是有效而快捷的,但由于作图误差的存在,所以设计精度较低。解析法是将运动设计问题用数学方程加以描述,通过方程的求解获得有关运动尺寸,故其直观性差,但设计精度高。随着数值计算方法的发展和计算机的普及应用,解析法已成为各类平面连杆机构运动设计的一种有效方法。
连杆机构_平面连杆机构 -基本特点
平面连杆机构
四杆机构基本型式四杆机构有两种基本类型。
①在满足曲柄存在的前提下,铰链四杆机构取不同的构件作机架,可得到具有不同运动特性的铰链四杆机构:例如曲柄摇杆机构,双曲柄机构和由它们派生出来的平行四边形机构,曲柄滑块机构等。铰链四杆机构中,若a为最短杆,取杆d或杆b为机架,则a为曲柄,c为摇杆,即得曲柄摇杆机构。如取a为机架,则b和d都是曲柄,即得双曲柄机构。
②在不满足曲柄存在的前提下,铰链四杆机构的运动链不论哪个杆固定,因无曲柄存在,必为双摇杆机构,取c为机架,b和d都是摇杆。如将曲柄摇杆机构的摇杆长度增加至无穷大,则转动副OB转化为移动副,即得曲柄滑块机构。此外四杆机构还带两个滑块型式的双滑块机构。
尺寸综合按给定的从动件运动来决定机构运动简图的尺寸。综合时尚应考虑最小传动角和曲柄存在等条件,以保证求得合理可靠的机构。
连杆机构_平面连杆机构 -尺寸综合
按给定的从动件运动来决定机构运动简图的尺寸。综合时尚应考虑最小传动角和曲柄存在等条件,以保证求得合理可靠的机构。
对从动件的运动要求是多种多样的,要综合的问题也各不相同。一般可归结为:①主动件运动规律一定时,要求从动件能实现给定的对应位置或近似实现给定函数的运动规律;②要求连杆能实现给定的位置;③要求连杆上某点能近似沿给定曲线运动。其中②是研究运动几何学的基本问题,据此也可求解近似实现给定曲线的机构。
尺寸综合的主要方法有解析法、图解法和实验法。①解析法:以函数逼近论为基础的代数法。这种方法精度高,计算繁复,但随着电子计算机的应用和向量、复数与矩阵等数学手段的运用,60年代以来发展很快,常用的有插值法、平方逼近法、最佳逼近法等。②图解法:以运动几何学为基础的几何方法。这种方法概念明确、简单,能以一定精度求解相当范围的问题,但精度不如解析法高,常用的有运动几何法和在其基础上提出的半角转动法等。③实验法:用不同机构参数的模型通过反复实验求解机构的尺寸(见机构综合)。
罗伯茨定理 若三个不同尺寸的铰链四杆机构O1O2B1A1、O2O3B2A2和O1O3B3A3(图3)间有下列关系:①O1A1ΜA3、O2B1ΜA2和O3B3ΜB2是铰链平行四边形;②ΔA1ΜB1∽ΔΜB2A2∽ΔA3B3Μ∽ΔO1O2O3,则在各自连杆上的Μ点可画出同一条曲线,称为罗伯茨定理。在综合再现给定轨迹的铰链四杆机构时,当设计出的机构不能满足传动角大小和安装位置等其他条件时,用罗伯茨定理可得出另两个不同尺寸的机构,以利于选择。
 爱华网
爱华网