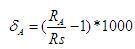换底公式是一个比较重要的公式,在很多对数的计算中都要使用,也是高中数学的重点。另有两个推论如下:log a(b)表示以a为底的b的对数。换底公式就是log(a)(b)=log(c)(b)/log(c)(a)(a,c均大于零且不等于1)。
换底公式_换底公式 -形式
换底公式换底公式是一个比较重要的公式,在很多对数的计算中都要使用,也是高中数学的重点。另有两个推论。
loga(b)表示以a为底的b的对数。
换底公式就是
log(a)(b)=log(c)(b)/log(c)(a)(a,c均大于零且不等于1)
换底公式_换底公式 -推导过程
若有对数log(a)(b)设a=n^x,b=n^y(n>0,且n不为1)如:log(10)(5)=log(5)(5)/log(5)(10)则log(a)(b)=log(n^x)(n^y)
根据对数的基本公式
log(a)(M^n)=nloga(M)和 基本公式log(a^n)M=1/n×log(a) M
易得
log(n^x)(n^y)=y/x
由a=n^x,b=n^y可得x=log(n)(a),y=log(n)(b)
则有:log(a)(b)=log(n^x)(n^y)=log(n)(b)/log(n)(a)
得证:log(a)(b)=log(n)(b)/log(n)(a)
例子:log(a)(c) * log(c)(a)=log(c)(c)/log(c)(a) *log(c)(a)=log(c)(c)=1
换底公式_换底公式 -应用
数学对数
在数学对数运算中,通常是不同底的对数运算,这时就需要换底。.通常在处理数学运算中,将一般底数转换为以e为底(即In)的自然对数或者是转换为以10为底(即lg)的常用对数,方便于我们运算;有时也通过用换底公式来证明或求解相关问题;
在计算器上计算对数时需要用到这个公式。例如,大多数计算器有[ln]和[log10]的按钮,但却没有[log2]的。要计算log2(3),你只有计算log10(3) / log10(2)(或 ln(3)/ln(2),两者结果一样);
工程技术
在工程技术中,换底公式也是经常用到的公式,例如,在编程语言中,有些编程语言(例如C语言)没有以a为底b为真数的对数函数;只有以常用对数10为底的对数或自然对数e为底的对数(即Ig、In),此时就要用到换底公式来换成以e或者10为底的对数来表示出以a为底b为真数的对数表达式,从而来处理某些实际问题。
 爱华网
爱华网