典型相关分析(canonical correlation analysis)就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。
典型相关分析_典型相关分析 -定义
典型相关分析(canonical correlation analysis)就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
典型相关分析_典型相关分析 -基本思想
典型相关分析方法canonical correlation analysis最早源于荷泰林H,Hotelling 。他所提出的方法于 1936 年在《生物统计》期刊上发表的一篇论文《两组变式之间的关系》经过多年的应用及发展,逐渐达到完善,在 70 年代臻于成熟。
由于典型相关分析涉及较大量的矩阵计算, 其方法的应用在早期曾受到相当的限制。但随着当代计算机技术及其软件的迅速发展,弥补了应用典型相关分析中的困难,因此它的应用开始走向普及化。 典型相关分析是研究两组变量之间相关关系的一种统计分析方法。
为了研究两组变量X 1 , X 2 ,…, X p 和 Y1 , Y2 ,…, Yq 之间的相关关系,采用类似于主成分分析的方法,在两组变量中,分别选取若干有代表性的变量组成有代表性的综合指标,通过研究这两组综合指标之间的相关关系,来代替这两组变量间的相关关系,这些综合指标称为典型变量。
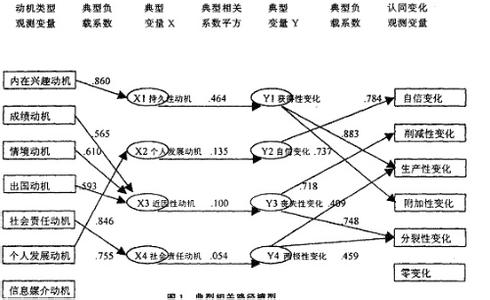
典型相关分析_典型相关分析 -数学描述
设有两随机变量组 X X 1 , X 2 ,…, X p ′ 和Y Y1 , Y2 ,…, Yq ′ ,不妨设 p ≤ q 。 对于 X , Y ,不妨设第一组变量的均值和协方差为矩阵为 E X 1 Cov X ∑ 11 第二组变量的均值和协方差为矩阵为 E Y 2 Cov Y ∑ 22 第一组与第二组变量的协方差为矩阵为 Cov X Y ∑ 12 ∑ 21 X 于是,对于矩阵 Z 有 (9―1―1) Y E X 1 均值向量 E Z E (9―1―2) E Y 2 ′ 协方差矩阵 ∑ E Z Z pq × pq E X X ′ ′ E X 1 Y 2 1 1 E Y X ′ ′ E Y 2 Y 2 2 1 ∑ 11 ∑ 12 p× p p×q ∑ 21 ∑ 22 q× p q× q 要研究两组变量 X 1 , X 2 ,…, X p 和 Y1 , Y2 ,…, Yq 之间的相关关系。
首先分别作两组变量的线性组合,即 U a1 X 1 a 2 X 2 L a p X p a ′X V b1Y1 b2Y2 L bq Yq b ′Y a a1 a 2 L a p , b b1 b2 L bq 分别为任意非零常系数向量,则 ′ ′可得, Var U a ′ Cov X a a ′ ∑ 11 a Var V b ′ Cov Y b b ′ ∑ 22 b Cov U V a ′ Cov X Y b a ′ ∑ 12 b 则称 U 与 V 为典型变量,它们之间的相关系数 ρ 称为典型相关系,即 a ′∑ 12 b ρ Corr U V a ′∑ 11 a b ′∑ 22 b 典型相关分析研究的问题是,如何选取典型变量的最优线性组合。
选取原则是:在所有 使得 U 1 a ′ X 1 1 1线性组合 U 和 V 中,选取典型相关系数为最大的 U 和 V ,即选取 a 和b与 V1 b ′ Y 之间的相关系数达到最大(在所有的 U 和 V 中) 1 2 2 ,然后选取 a 和b 使得U 2 a ′ 2 X 与 V2 b′ 2Y 的相关系数在与 U 1 和 V1 不相关的组合 U 和 V 中最大,继续下去,直到所有分别与 U 1 U 2 LU p 1 和 V1 V2 LV p 1 ,都不相关的线性组合 U p , p 为止。
V 此时 p等于诸变量 X 与 Y 之间的协方差矩阵的秩。 典型变量 U 1 和 V1 , U 2 和 V2 …… U p 和 V p 是根据它们的相关系数由大列小逐对提取,直到两组变量之间的相关性被分解完毕为止。
典型相关分析_典型相关分析 -典型变量与典型相关系数的求法
(一)总体典型变量与典型相关系数 由上一节的数学描述我们知道,典型相关分析希望寻求 a 和 b 使得 ρ 达到最大,但是由于随机变量乘以常数时不改变它们的相关系数,为了防止不必要的结果重复出现,最好的限制是令 Var U 1 和 Var V 1。
于是,我们的问题就转化为,在约束条件为 Var U 1和 Var V 1 下,寻找非零常数向量 a 和 b 使得相关系数 Corr U V a ′ ∑ 12 b 达到最大。 根据数学分析中条件极值的求法,引入拉格朗日(Lagrange)乘数,问题则转化为,求 λ ν φ a b a ′ ∑ 12 b 2 a′∑ 11 a 1 2 b′∑ 11 b 1 的极大值点,其中 λ ν 是拉格朗日乘数。
由极值的必要条件,需求 φ 对 a 和 b 的偏导数,并令其等于零,得到的极值条件为: φ a ∑12 b λ ∑11 a 0 φ ∑ a ν ∑ b 0 b 21 22 将分别以 a ′ 和 b ′ 左乘上式,得 a ′ ∑12 b λa ′∑11 a λ b′ ∑ 21 a νb′∑22 b ν又因为 a ′ ∑12 b′ b ′ ∑ 12 a, 故 λ ν a′ ∑ 12 bρ , 说明, λ 的值就是线性组合 U 和 V 之间的相关系数。
因此上述方程可写成: λ ∑11 a ∑12 b 0 ∑ 21 a λ ∑22 b 0 为求解方程,先以 ∑ ∑12 1 22 左乘以上述第二式,并将第一式代入,得 ∑ 12 ∑ 1 ∑ 21 λ2 ∑11 a 0 22 同理,将 ∑ ∑ 21 1 11 左乘以上述第一式,并将第二式代入,得 ∑ 21 ∑ 111 ∑ 12 λ2 ∑22 b 0 将上边两式分别左乘以 ∑ 1 11 和 ∑ 1 22 ,得 ∑ 1 11 ∑ ∑ ∑ 12 1 22 21 λ2 a0 ∑1 ∑ 21 ∑ 11 ∑ 12 λ2 b 0 22 1 令 A ∑ ∑ ∑ ∑ 1 11 12 1 22 21 B ∑ ∑ ∑ ∑ 1 22 21 1 11 12 则得 Aa λ a 2 Bb λ2 b 说明, λ 既是矩阵 A ,同时也是矩阵 B 的特征值,同时也表明,相应的 a 与 b 分别是 2特征值 λ 的特征向量。 2 而且,根据证明,矩阵 A 和 B 的特征值还具有以下的性质:
(1)矩阵 A 和 B 有相同的非零特征值,且相等的非零特征值的数目就等于 p 。
(2)矩阵 A 和 B 的特征值非负。
(3)矩阵 A 和 B 的全部特征值均在 0 和 1 之间。 根据前边,我们知道,λ ν a ′ ∑12 b ρ ,所以 λ 为其典型变量 U 和 V 之间的简单相关系数。 又由于要求其相关系数达到最大按习惯考虑为正相关,所以取矩阵 A 或 B 的最大特征值 λ1 的平方根 λ1 。
作为相关系致,同时由特征值 λ1 所对应的两个特征向量 a 2 2 1 1 和b 有: U 1 a ′ 1 X 和 V1 b′ 1Y这就是所要选取的第一对线性组合,也即第一对典型变量,它们在所有的线性组合 U 和 V 中具有有最大的相关系数 λ1 。 若求出矩阵 A 或 B 的 p 个非零特征根( p 是矩阵 ∑12 的秩,这里实际上 p q ) ,设为 λ1 ≥ λ2 ≥ L ≥ λ2 ≥ 0 2 2 p 1 2 相应的特征向量是与 a a L a k 和 b 1 b 2 L b k ,则可得 k 对线性组合: U 1 a11 X 1 a 21 X 2 L a p1 X p 2 2 2 U 2 a1 X 1 a 2 X 2 L a p X p M k k U p a1 X 1 a 2 X 2 L a pk X p 和 V1 b11Y1 b21Y2 L bq1Yq 2 2 2 V2 b1 Y1 b2 Y2 L bq Yq M k k V p b1 Y1 b2 Y2 L bqk Yq 它们的相关系数为 λ1 ≥ λ 2 ≥
典型相关分析_典型相关分析 -应用
典型相关分析的用途很广。在实际分析问题中,当我们面临两组多变量数据,并希望研究两组变量之间的关系时,就要用到典型相关分析。 例如,为了研究扩张性财政政策实施以后对宏观经济发展的影响,就需要考察有关财政政策的一系列指标如财政支出总额的增长率、财政赤字增长率、国债发行额的增长率、税率降低率等与经济发展的一系列指标如国内生产总值增长率、就业增长率、物价上涨率等两组变量之间的相关程度。
又如,为了研究宏观经济走势与股票市场走势之间的关系,就需要考察各种宏观经济指标如经济增长率、失业率、物价指数、进出口增长率等与各种反映股票市场状况的指标如股票价格指数、股票市场融资金额等两组变量之间的相关关系。再如,工厂要考察所使用的原料的质量对所生产的产品的质量的影响,就需要对所生产产品的各种质量指标与所使用的原料的各种质量指标之间的相关关系进行测度。
又如,在分析评估某种经济投入与产出系统时,研究投入和产出情况之间的联系时,投入情况面可以从人力、物力等多个方面反映,产出情况也可以从产值、利税等方面反映; 再如在分析影响居民消费因素时,我们可以将劳动者报酬、家庭经营收入、转移性收入等变量构成反映居民收入的变量组,而将食品支出、医疗保健支出、交通和通讯支出等变量构成反映居民支出情况的变量组,然后通过研究两变量组之间关系来分析影响居民消费因素情况。典型相关分析 先将较多变量转化为少数几个典型变量,再通过其间的典型相关系数来综合描述两组多元随机变量之间关系的统计方法。设x是p元随机变量,y是q元随机变量,如何描述它们之间的相关程度?当然可逐一计算x的p个分量和y的q个分量之间的相关系数(p×q个), 但这样既繁琐又不能反映事物的本质。如果运用典型相关分析,其基本程序是,从两组变量各自的线性函数中各抽取一个组成一对,它们应是相关系数达到最大值的一对,称为第1对典型变量,类似地还可以求出第2对、第3对、……,这些成对变量之间互不相关,各对典型变量的相关系数称为典型相关系数。所得到的典型相关系数的数目不超过原两组变量中任何一组变量的数目。
典型相关分析有助于综合地描述两组变量之间的典型的相关关系。其条件是,两组变量都是连续变量,其资料都必须服从多元正态分布。
以上几种多元分析方法各有优点和局限性。每一种方法都有它特定的假设、条件和数据要求,例如正态性、线性和同方差等。因此在应用多元分析方法时,应在研究计划阶段确定理论框架,以决定收集何种数据、怎样收集和如何分析数据资料。
 爱华网
爱华网