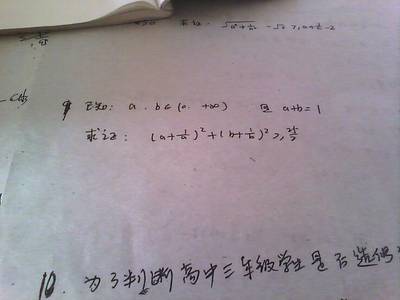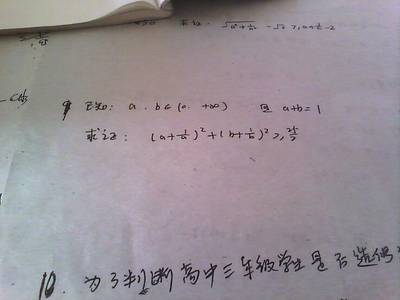《用配方法证明》证明书
用配方法证明设矩形长为x,那么宽为15-x
面积S=x(15-x)=-x^2+15x=-(x-7.5)^2+56.25≤56.25
所以面积最大为56.25平方米,无法达到60平方米
x-12x+40=x-12x+36+4 =(x-6)^2+4因为(X-6)^2≥0所以(X-6)^2+4≥4所以大于0要原式的值最小从(X-6)^2+4≥4看出最小值为4当(X-6)^2=0时 也就是X=6时取得
2
4x²-6x+11=(2x)²-6x+(1.5)²+8.75=(2x-1.5)²+8.75显然(2x-1.5)²+8.75>=8。75x=0.75时 最小值8.75继续追问: 解一下 0.4x的平方-0.5x-1+03解:y2-2√2y=-√5(文章阅读网:www.www.AihuAu.com.net )
y2-2√2y+2=-√5+2
(y-2)的平方=-√5+2(负数)
所以一定大于的,否则就是虚数解了!!!4y2-2×√2 ×y+√5
解:y2-2√2y=-√5
y2-2√2y+2=-√5+2
(y-2)的平方=-√5+2(负数)
所以一定大于的,否则就是虚数解了!!!
昨天大错了。今天改好了。
不为0的某数的平方一定大于0!!! 5y^2-2×√2 ×y+√5
解:原式=(y-√2 )^2+√5-2
因为(y-√2 )^2大于等于0
且√5大于2
所以(y-√2 )^2+√5-2恒大于0
即可证y^2-2×√2 ×y+√5恒大与零
6
证明:
-3x²-x+1
=-3(x²+1/3x)+1
=-3(x²+1/3x+1/36)+1/12+1
=-3(x+1/6)²+13/12
因为-3(x+1/6)²≤0,所以-3(x+1/6)²+13/12≤13/12

所以
-3x²-x+1的值不大于13/12
7
2x^2+5x-1-(x^2+8x-4); =x^2-3x+3 ;=(x-3/2)^2+3/4; 因为(x-3/2)^2>=0; 所以2x^2+5x-1-(x^2+8x-4)>=3/4; 因此不论X取何值时,代数式2X^2+5X-1的值总比X^2+8X-4的值大;X=3/2时,两代数式的差最小,为3/4; 希望能够帮助你!! 4(3x-1)^2-9(3X+1)^2=0;移相:4(3x-1)^2=9(3X+1)^2;开平方:2(3x-1)=3(3X+1); 6x-2=9x+3; -5=3x; x= - 5/3;
8
X―12X+40=x-2*6x+36+4=(x-6)^2+4因为(X-6)^2=>0所以X―12X+40的值大于等于4当(X-6)=0;即X=6时(X-6)^2+4=4所以当X等于6时代数式的最小值。
9
X的平方―12X+40=x的平方-2*6X+6的平方+4=(X-6)的平方+4因为(X-6)的平方一定大于0或等于0所以代数式X的平方―12X+40的值大于4X等于6时代数式的最小值
10
-2x^2+4x-5
=-2(X²-2X)-5
=-2(X²-2X+1-1)-5
=-2(X-1)²+2-5
=-2(X-1)²-3
因为(X-1)²≥0,所以-2(X-1)²≤0
故-2(X-1)²-3≤-3
所以代数式-2x^2+4x-5的值恒小于零
若有疑问可以追问、
 爱华网
爱华网