霍夫变换是图像处理中识别几何形状的一种方法,在图像处理中有着广泛应用,霍夫变换不受图形旋转的影响,易于进行几何图形的快速变换。基于霍夫变换的改进方法也有很多,其中一个重要的方法是广义霍夫变换,可以用来检测任意形状的曲线。
霍夫变换(Hough Transform) 是通过在参数空间进行统计的方法进行鲁棒参数估计的一种算法。霍夫变换_霍夫变换 -基本原理
霍夫变换是图像处理中从图像中识别几何形状的基本方法之一,应用很广泛,也有很多改进算法。最基本的霍夫变换是从黑白图像中检测直线(线段)。
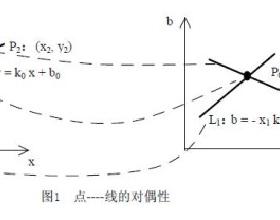
我们先看这样一个问题:设已知一黑白图像上画了一条直线,要求出这条直线所在的位置。我们知道,直线的方程可以用 y = k*x + b 来表示,其中k和b是参数,分别是斜率和截距。过某一点 (x0,y0) 的所有直线的参数都会满足方程 y0=kx0+b。即点(x0,y0)确定了一族直线。方程 y0=kx0+b 在参数 k--b 平面上是一条直线,(你也可以是方程 b=-x0*k+y0对应的直线)。这样,图像 x--y 平面上的一个前景像素点就对应到参数平面上的一条直线。我们举个例子说明解决前面那个问题的原理。设图像上的直线是 y=x, 我们先取上面的三个点:A(0,0), B(1,1), C(22)。可以求出,过 A 点的直线的参数要满足方程 b=0, 过 B 点的直线的参数要满足方程 1=k+b, 过 C 点的直线的参数要满足方程 2=2k+b, 这三个方程就对应着参数平面上的三条直线,而这三条直线会相交于一点 (k=1,b=0)。 同理,原图像上直线 y=x 上的其它点(如(3,3),(4,4)等) 对应参数平面上的直线也会通过点(k=1,b=0)。这个性质就为我们解决问题提供了方法:
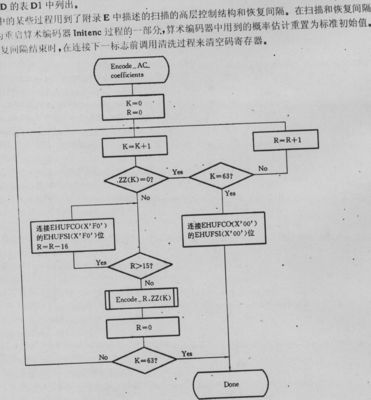
1. 首先,我们初始化一块缓冲区,对应于参数平面,将其所有数据置为 0.
2. 对于图像上每一前景点,求出参数平面对应的直线,把这直线上的所有点的值都加 1。
3. 最后,找到参数平面上最大点的位置,这个位置就是原图像上直线的参数。
上面就是霍夫变换的基本思想。就是把图像平面上的点对应到参数平面上的线,最后通过统计特性来解决问题。假如图像平面上有两条直线,那么最终在参数平面上就会看到两个峰值点,依此类推。
在实际应用中,y=k*x+b 形式的直线方程没有办法表示 x=c 形式的直线(这时候,直线的斜率为无穷大)。所以实际应用中,是采用参数方程 p=x*cos(theta)+y*sin(theta)。这样,图像平面上的一个点就对应到参数 p---theta 平面上的一条曲线上。其它的还是一样。
再看下面一个问题:我们要从一副图像中检测出半径以知的圆形来。这个问题比前一个还要直观。我们可以取和图像平面一样的参数平面,以图像上每一个前景点为圆心,以已知的半径在参数平面上画圆,并把结果进行累加。最后找出参数平面上的峰值点,这个位置就对应了图像上的圆心。在这个问题里,图像平面上的每一点对应到参数平面上的一个圆。
把上面的问题改一下,假如我们不知道半径的值,而要找出图像上的圆来。这样,一个办法是把参数平面扩大称为三维空间。就是说,参数空间变为x--y--R三维,对应圆的圆心和半径。
图像平面上的每一点就对应于参数空间中每个半径下的一个圆,这实际上是一个圆锥。最后当然还是找参数空间中的峰值点。不过,这个方法显然需要大量的内存,运行速度也会是很大问题。
有什么更好的方法么?我们前面假定的图像都是黑白图像(2值图像),实际上这些2值图像多是彩色或灰度图像通过边缘提取来的。我们前面提到过,图像边缘除了位置信息,还有方向信息也很重要,这里就用上了。根据圆的性质,圆的半径一定在垂直于圆的切线的直线上,也就是说,在圆上任意一点的法线上。这样,解决上面的问题,我们仍采用2维的参数空间,对于图像上的每一前景点,加上它的方向信息,都可以确定出一条直线,圆的圆心就在这条直线上。这样一来,问题就会简单了许多。
接下来还有许多类似的问题,如检测出椭圆,正方形,长方形,圆弧等等。这些方法大都类似,关键就是需要熟悉这些几何形状的数学性质。霍夫变换的应用是很广泛的,比如我们要做一个支票识别的任务,假设支票上肯定有一个红颜色的方形印章,我们可以通过霍夫变换来对这个印章进行快速定位,在配合其它手段进行其它处理。霍夫变换由于不受图像旋转的影响,所以很容易的可以用来进行定位。
霍夫变换_霍夫变换 -广义霍夫变换
霍夫变换有许多改进方法,一个比较重要的概念是广义霍夫变换,它是针对所有曲线的,用处也很大。就是针对直线的霍夫变换也有很多改进算法,比如前面的方法我们没有考虑图像上的这一直线上的点是否连续的问题,这些都要随着应用的不同而有优化的方法。
 爱华网
爱华网