线性常微分方程是微分方程中出现的未知函数和该函数各阶导数都是一次的，称为线性常微分方程。它的理论是常微分方程理论中基本上完整、在实际问题中应用很广的一部份。
线性微分方程_线性常微分方程 -线性常微分方程
线性微分方程_线性常微分方程 -正文
微分方程中出现的未知函数和该函数各阶导数都是一次的，称为线性常微分方程。它的理论是常微分方程理论中基本上完整、在实际问题中应用很广的一部份。y┡+p(x)y=Q(x) (1)
及其对应的齐次线性方程y┡+p(x)y=0 (2)
的解法，得到(2)的通解和满足初始条件y(x0)=y0的特解分别为：
(3)
， (4)
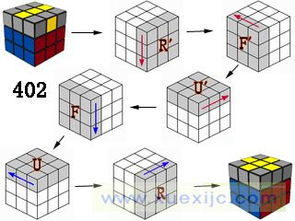
二阶魔方的玩法——欢迎来到二阶魔方玩法如果觉得下面的方法有点复杂的话,请看它的简易解法http://www.360doc.com/showWeb/0/0/58577046.aspx在这里我们将讨论二阶魔方的玩法，介绍如何还原二阶魔方，二阶魔方的玩法非常容易学，在这个教
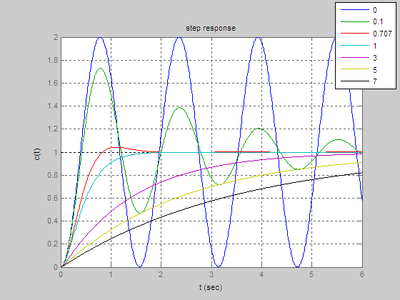
二阶系统的标准形式为：C（s）/G(s)=wn^2/s^2+2*wn*zeta*s+wn^2;利用matlab仿真分析zeta取不同值时的单位阶跃响应程序如下：clear clfwn=2;t=0:0.01:20for zeta=[0:0.2:1.2]s=tf(4,[1,4*zeta,4]);figure(1),step(s,t),hold onend
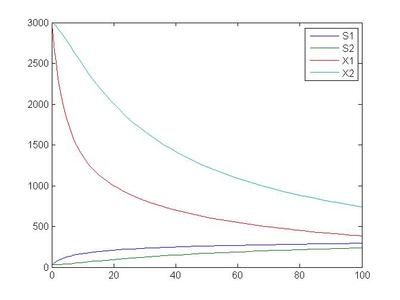
实验四 求微分方程的解一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景与实验目的实际应用问题通过数学建模所归纳而得到的方程，绝大多数都是微分方程，真正能得到代数方程的机会很少．另一方面，能够
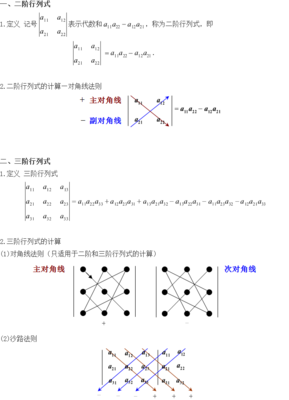
线性代数一：二阶和三阶行列式对于初中所学的二元线性方程组，我们可以通过加减法或者是消元法得出结果。运用消元法消去方程组中的未知数，就可以得到二元线性方程组的解。但是我们可以编造一套算法来简化这种计算，即把每个二元线性方程
齿轮魔方是个很神奇的魔方……一代拿到手里时，第一天没弄明白，第二天诡异的复原了，而后有人总结上下左右转法，开始没难度了；二代刚出趁热也能复原了，之后闲置了几个月，再拿来就怎么也复原不了。然后有人提出了三代构想，就是吧无齿轮棱变为八
爱华网