发布时间:2018年04月10日 20:03:44分享人:沵像个迷来源:互联网28
基本初等函数 - 定义所谓初等函数就是由基本初等函数经过有些次的四则运算和复合而成的函数。是由基本初等函数经过有限次的有理运算和复合而成的并且可用一个式子表示的函数。基本初等函数和初等函数在其定义区间内均为连续函数。不是初等函数的函数,称为非初等函数,如狄利克雷函数和黎曼函数。
初等函数_基本初等函数 -常值函数
(也称常数函数) y =c(其中c 为常数)初等函数_基本初等函数 -幂函数
y =x a(其中a 为实常数)
初等函数_基本初等函数 -指数函数
y =a x(a>0,a≠1)
初等函数_基本初等函数 -对数函数
y =logax(a>0,a≠1)
初等函数_基本初等函数 -三角函数
正弦函数
y =sinx
余弦函数
y =cosx
正切函数
y =tanx(也记成y =tgx)
余切函数
y =cotx(也记成y =ctgx)
正割函数
y =secx
余割函数
y =cscx
反三角函数
反正弦函数 y =arcsinx
反余弦函数 y =arccosx
反正切函数 y =arctanx
反余切函数y =arccotx
(反正割函数、反余割函数一般不用)
初等函数_基本初等函数 -定义
所谓初等函数就是由基本初等函数经过有些次的四则运算和复合而成的函数。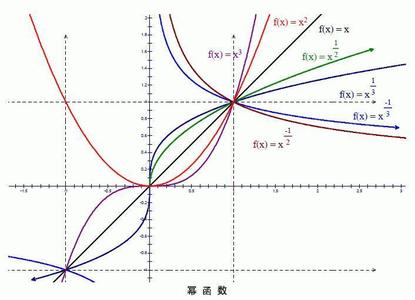
爱华网本文地址 » http://www.aihuau.com/a/8103420103/93328.html
更多阅读
安徽省铜陵市第三中学 柏永红一, 教材分析幂函数这节内容,在高中数学教材中可以说是几起几落,由于它的图象多样性和复杂性(图象有11种),在“减负”的呼声中几次被删除。随着网络计算机的发展,一些先进的数学软件不断涌现,利用信息技术探索幂
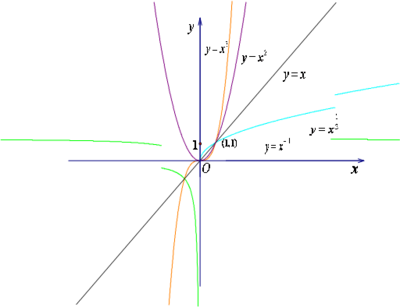
幂函数教案(第一课时)太湖县徐桥高中王志余教材分析:幂函数模型在生活中是比较常见的,学习时结合生活中的具体实例来引出常见的幂函数y=x,y=x2,y=x3,y=x-1,y=x1/2。组织学生画出他们的图象,根据图象观察、总结这几个常见幂函数的性质
____与刘峰先生商讨 看了刘先生的<谈谈利润及其来源>,觉得意见相左,回了一贴.意犹未尽,相再发一主贴详尽地说一下我的观点. 首先我们来看一下会计学上的利润观.某人以100元买进某商品,再以120元卖出,如果先不考虑其它费
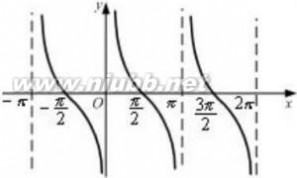
表示时用“cot+角度”,如:30°的余切表示为cot30°;角A的余切表示为cotA 旧用ctgA来表示余切,至今仍在使用,和cotA是一样的。(注:现在已经不常用了)任意角中边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原

 爱华网
爱华网



