《叙述并证明余弦定理》证明书
叙述并证明余弦定理余弦定理(第二余弦定理)余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值
编辑本段余弦定理性质
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质――
a^2 = b^2+ c^2 - 2・b・c・cosA
b^2 = a^2 + c^2 - 2・a・c・cosB(散文阅读:www.www.AihuAu.com.net )
c^2 = a^2 + b^2 - 2・a・b・cosC
cosC = (a^2 + b^2 - c^2) / (2・a・b)
cosB = (a^2 + c^2 -b^2) / (2・a・c)
cosA = (c^2 + b^2 - a^2) / (2・b・c)
(物理力学方面的平行四边形定则中也会用到)
第一余弦定理(任意三角形射影定理)
设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有
a=b・cos C+c・cos B, b=c・cos A+a・cos C, c=a・cos B+b・cos A。
编辑本段余弦定理证明
平面向量证法
∵如图,有a+b=c(平行四边形定则:两个邻边之间的对角线代表两个邻边大小) ∴c・c=(a+b)・(a+b)
∴c^2=a・a+2a・b+b・b∴c^2=a^2+b^2+2|a||b|Cos(π-θ)
(以上粗体字符表示向量)
又∵Cos(π-θ)=-Cosθ
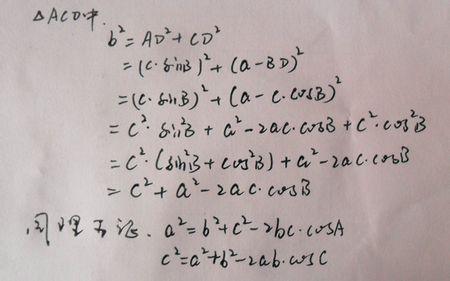
∴c2=a2+b2-2|a||b|Cosθ(注意:这里用到了三角函数公式)
再拆开,得c2=a2+b2-2*a*b*CosC
即 CosC=(a2+b2-c2)/2*a*b
同理可证其他,而下面的CosC=(c2-b2-a2)/2ab就是将CosC移到左边表示一下。
平面几何证法
在任意△ABC中
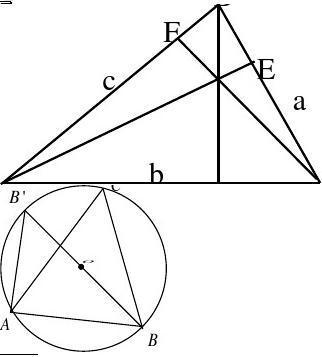
做AD⊥BC.
∠C所对的边为c,∠B所对的边为b,∠A所对的边为a
则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c
根据勾股定理可得:
AC2=AD2+DC2
b2=(sinB*c)2+(a-cosB*c)2
b2=(sinB*c)2+a2-2ac*cosB+(cosB)2*c2
b2=(sinB2+cosB2)*c2-2ac*cosB+a2
b2=c2+a2-2ac*cosB
cosB=(c2+a2-b2)/2ac
编辑本段作用
(1)已知三角形的三条边长,可求出三个内角
(2)已知三角形的两边及夹角,可求出第三边。
(3)已知三角形两边及其一边对角,可求其它的角和第三条边。(见解三角形公式,推导过程略。)
判定定理一(两根判别法):
若记m(c1,c2)为c的两值为正根的个数,c1为c的表达式中根号前取加号的值,c2为c的表达式中根号前取
减号的值
①若m(c1,c2)=2,则有两解
②若m(c1,c2)=1,则有一解
③若m(c1,c2)=0,则有零解(即无解)。
注意:若c1等于c2且c1或c2大于0,此种情况算到第二种情况,即一解。
判定定理二(角边判别法):
一当a>bsinA时
①当b>a且cosA>0(即A为锐角)时,则有两解
②当b>a且cosA<=0(即A为直角或钝角)时,则有零解(即无解)
③当b=a且cosA>0(即A为锐角)时,则有一解
④当b=a且cosA<=0(即A为直角或钝角)时,则有零解(即无解)
⑤当b 二当a=bsinA时
①当cosA>0(即A为锐角)时,则有一解
②当cosA<=0(即A为直角或钝角)时,则有零解(即无解)
三当a 例如:已知△ABC的三边之比为5:4:3,求最大的内角。
解 设三角形的三边为a,b,c且a:b:c=5:4:3.
由三角形中大边对大角可知:∠A为最大的角。由余弦定理
cos A=0
所以∠A=90°.
再如△ABC中,AB=2,AC=3,∠A=60度,求BC之长。
解 由余弦定理可知
BC2=AB2+AC2-2AB×AC・cos A
=4+9-2×2×3×cos60
=13-12x0.5
=13-6
=7
所以BC=√7. (注:cos60=0.5,可以用计算器算)
以上两个小例子简单说明了余弦定理的作用。
编辑本段其他
从余弦定理和余弦函数的性质可以看出,如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角一定是直角,如果小于第三边的平方,那么第三边所对的角是钝角,如果大于第三边的平方,那么第三边所对的角是锐角。即,利用余弦定理,可以判断三角形形状。同时,还可以用余弦定理求三角形边长取值范围。
解三角形时,除了用到余弦定理外还常用正弦定理。
 爱华网
爱华网