《正弦定理的证明方法》证明书
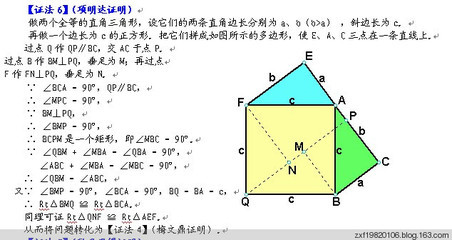
正弦定理的证明方法如图1,△ABC中,AD平分乙A交BC于D,由三角形内角平分线有AB BDAC一DC由正弦定理有:由(1)(2)(3,得:韶=韶幼朋=Ac:.△ABc为等腰三角形。证明‘三角证法,:BE平分匕B二器二黯…(l)AB AC AB滋nC舀石乙二蕊丽劝元二舀丽””’‘(2)CF平分二C幼器二默…(2);EF//BC
用余弦定理:a^2+b^2-2abCOSc=c^2
COSc=(a^2+b^2-c^2)/2ab
SINc^2=1-COSc^2
SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2
=[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2(文章阅读网:www.www.AihuAu.com.net )
同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2
得证
正弦定理:三角形ABC中 BC/sinA=AC/sinB=AB/sinC
证明如下:在三角形的外接圆里证明会比较方便
例如,用BC边和经过B的直径BD,构成的直角三角形DBC可以得到:
2RsinD=BC (R为三角形外接圆半径)
角A=角D
得到:2RsinA=BC
同理:2RsinB=AC,2RsinC=AB
这样就得到正弦定理了
2
一种是用三角证asinB=bsinA
用面积证
用几何法,画三角形的外接圆
听说能用向量证,咋么证呢?
三角形ABC为锐角三角形时,过A作单位向量j垂直于向量AB,则j 与向量AB夹角为90,j与向量BC夹角为(90-B),j与向量CA夹角为(90+A),设AB=c,BC=a,AC=b,
因为AB+BC+CA=0
即j*AB+J*BC+J*CA=0
|j||AB|cos90+|j||BC|cos(90-B)+|j||CA|cos(90+A)=0
所以asinB=bsinA
3
用余弦定理:a^2+b^2-2abCOSc=c^2

COSc=(a^2+b^2-c^2)/2ab
SINc^2=1-COSc^2
SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2
=[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2
同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2
得证用余弦定理:a^2+b^2-2abCOSc=c^2 COSc=(a^2+b^2-c^2)/2ab SINc^2=1-COSc^2 SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2 =[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2 同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2 得证
4
满意答案 好评率:100%
正弦定理
步骤1.
在锐角△ABC中,设BC=a,AC=b,AB=c。作CH⊥AB垂足为点H
CH=a・sinB
CH=b・sinA
∴a・sinB=b・sinA
得到 a/sinA=b/sinB
同理,在△ABC中, b/sinB=c/sinC
步骤2.
证明a/sinA=b/sinB=c/sinC=2R:
如图,任意三角形ABC,作ABC的外接圆O.
作直径BD交⊙O于D.
连接DA.
因为直径所对的圆周角是直角,所以∠DAB=90度
因为同弧所对的圆周角相等,所以∠D等于∠C.
所以c/sinC=c/sinD=BD=2R 类似可证其余两个等式。
余弦定理
平面向量证法:
∵如图,有a+b=c(平行四边形定则:两个邻边之间的对角线代表两个邻边大小)
∴c・c=(a+b)・(a+b)
∴c^2=a・a+2a・b+b・b∴c^2=a^2+b^2+2|a||b|Cos(π-θ)
(以上粗体字符表示向量)
又∵Cos(π-θ)=-CosC
∴c^2=a^2+b^2-2|a||b|Cosθ(注意:这里用到了三角函数公式)
再拆开,得c^2=a^2+b^2-2*a*b*CosC
同理可证其他,而下面的CosC=(c^2-b^2-a^2)/2ab就是将CosC移到左边表示一下。
平面几何证法:
在任意△ABC中
做AD⊥BC.
∠C所对的边为c,∠B所对的边为b,∠A所对的边为a
则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c
根据勾股定理可得:
AC^2=AD^2+DC^2
b^2=(sinB*c)^2+(a-cosB*c)^2
b^2=sinB²・c²+a^2+cosB²・c^2-2ac*cosB
b^2=(sinB^2+cosB^2)*c^2-2ac*cosB+a^2
b^2=c^2+a^2-2ac*cosB
cosB=(c^2+a^2-b^2)/2ac
 爱华网
爱华网