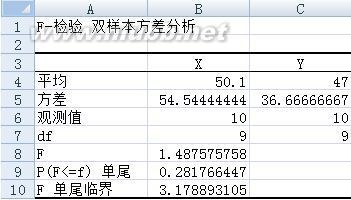
F―检验法是检验两个正态随机变量的总体方差是否相等的一种假设检验方法。
F―检验法是检验两个正态随机变量的总体方差是否相等的一种假设检验方法。设两个随机变量X、Y的样本分别为X1,x2,……,xn与y1,y2,……,yn,其样本方差分别为s1^2与s2^2。现检验X的总体方差DX与Y的总体方差DY是否相等。假设H0:DX=DY=σ^2。根据统计理论,如果X、Y为正态分布,当假设成立时,统计量(如右图)服从第一自由度为n1―1、第二自由度n2―1的F―分布。预先给定信度α。查F―分布表,得Fα/2。若计算的F值小于Fα/2,则假设成立,否则假设不合理。F―检验法还可用于两个以上随机变量平均数差异显著性的检验。F检验法是英国统计学家Fisher提出的,主要通过比较两组数据的方差 S^2,以确定他们的精密度是否有显著性差异。至于两组数据之间是否存在系统误差,则在进行F检验并确定它们的精密度没有显著性差异之后,再进行t 检验。
样本标准偏差的平方,即(“^2”是表示平方):
S^2=∑(X-X平均)^2/(n-1)
两组数据就能得到两个S^2值,S大^2和S小^2
F=S大^2/S小^2
由表中f大和f小(f为自由度n-1),查得F表,
然后计算的F值与查表得到的F表值比较,如果
F < F表 表明两组数据没有显著差异;
F ≥ F表 表明两组数据存在显著差异
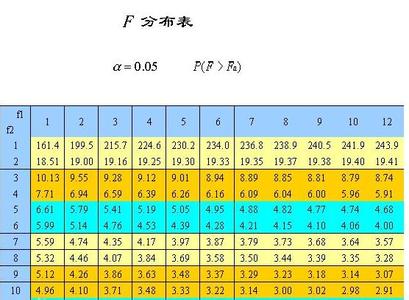
置信度95%时F值(单边)
f大
f小2345678910∞2
3
4
5
6
7
8
9
10
∞19.0
9.55
6.94
5.79
5.14
4.74
4.46
4.26
4.10
3.0019.16
9.28
6.59
5.41
4.76
4.35
4.07
3.86
3.71
3.6019.25
9.12
6.39
5.19
4.53
4.12
3.84
3.63
3.48
2.3719.30
9.01
6.26
5.05
4.39
3.97
3.69
3.48
3.33
3.2119.33
8.94
6.16
4.95
4.28
3.87
3.58
3.37
3.22
2.1019.36
8.88
6.09
4.88
4.21
3.79
3.50
3.29
3.14
2.0119.37
8.84
6.04
4.82
4.51
3.73
3.44
3.23
3.07
1.9419.38
8.81
6.00
4.78
4.10
3.68
3.39
3.18
3.02
1.8819.39
8.78
5.96
4.74
4.06
3.63
3.34
3.13
2.97
1.8319.5
8.53
5.63
4.36
3.67
3.23
2.93
2.71
2.54
1.00为大方差数据的自由度; 为小方差数据的自由度。
 爱华网
爱华网