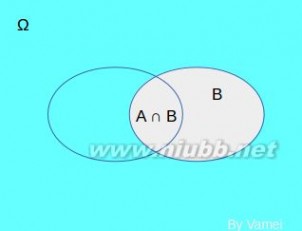
条件概率,是指在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么下一个随机选择的元素属于A的概率就定义为在B的前提下A的条件概率。当且仅当两个随机事件A与B满足P(A∩B)=P(A)P(B)的时候,它们才是统计独立的,这样联合概率可以表示为各自概率的简单乘积。同样,对于两个独立事件A与B,如果A与B是相互独立的,那么A在B这个前提下的条件概率就是A自身的概率;同样,B在A的前提下的条件概率就是B自身的概率。
条件概率_条件概率 -概念
条件概率公式
P(A|B) = P(AB)/P(B)
条件概率示例:就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
联合概率:表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B)。
边缘概率:是某个事件发生的概率,而与其它事件无关。边缘概率是这样得到的:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率)。这称为边缘化(marginalization)。A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
需要注意的是,在这些定义中A与B之间不一定有因果或者时间顺序关系。A可能会先于B发生,也可能相反,也可能二者同时发生。A可能会导致B的发生,也可能相反,也可能二者之间根本就没有因果关系。例如考虑一些可能是新的信息的概率条件性可以通过贝叶斯定理实现。
条件概率_条件概率 -基本定理
定理1
设A,B是两个事件,且A不是不可能事件,则称为在事件A发生的条件下,事件B发生的条件概率。一般地,,且它满足以下三条件:
(1)非负性;(2)规范性;(3)可列可加性。
定理2
设E为随机试验,Ω为样本空间,A,B为任意两个事件,设P(A)>0,称为在“事件A发生”的条件下事件B的条件概率。
上述乘法公式可推广到任意有穷多个事件时的情况。
设A1,A2,…An为任意n个事件(n2)且P(A1A2…An-1)>0,则P(A1A2…An)=P(A1)P(A2|A1)…P(An|A1A2…An-1)
定理3(全概率公式1)
设B1,B2,…Bn是一组事件,若(1)BiBj≠j,i≠j,i,j=1,2,…,n;(2)B1∪B2∪…∪Bn=Ω则称B1,B2,…Bn样本空间Ω的一个部分,或称为样本空间Ω的一个完备事件组。
定理4(全概率公式2)
设事件组B1,B2是样本空间Ω的一个划分,且P(Bi)>0(i=1,2,…n),则对任一事件B,有
定理5(贝叶斯公式)
设A1,A2,…An…是一完备事件组,则对任一事件B,P(B)>0,有
条件概率_条件概率 -统计独立性
当且仅当两个随机事件A与B满足
P(A∩B)=P(A)P(B)
的时候,它们才是统计独立的,这样联合概率可以表示为各自概率的简单乘积。
同样,对于两个独立事件A与B有
P(A|B)=P(A)
以及
P(B|A)=P(B)
换句话说,如果A与B是相互独立的,那么A在B这个前提下的条件概率就是A自身的概率;同样,B在A的前提下的条件概率就是B自身的概率。
条件概率_条件概率 -互斥性
当且仅当A与B满足 P(A∪B)=P(A)+P(B)且 P(A∩B)=0, 的时候,A与B是互斥的。
因此,换句话说,如果B已经发生,由于A不能B在同一场合下发生,那么A发生的概率为零;同样,如果A已经发生,那么B发生的概率为零。
条件概率_条件概率 -其它
如果事件B的概率P(B) > 0,那么Q(A) =P(A|B) 在所有事件A上所定义的函数Q就是概率测度。 如果P(B) = 0,P(A|B) 没有定义。 条件概率可以用决策树进行计算。条件概率_条件概率 -条件概率谬论
条件概率的谬论是假设P(A|B) 大致等于P(B|A)。数学家John Allen Paulos 在他的《数学盲》一书中指出医生、律师以及其他受过很好教育的非统计学家经常会犯这样的错误。这种错误可以通过用实数而不是概率来描述数据的方法来避免。P(A|B) 与P(B|A)的关系如下所示:
下面是一个虚构但写实的例子,P(A|B) 与P(B|A)的差距可能令人惊讶,同时也相当明显。
若想分辨某些个体是否有重大疾病,以便早期治疗,我们可能会对一大群人进行检验。虽然其益处明显可见,但同时,检验行为有一个地方引起争议,就是有检出假阳性的结果的可能:若有个未得疾病的人,却在初检时被误检为得病,他可能会感到苦恼烦闷,一直持续到更详细的检测显示他并未得病为止。而且就算在告知他其实是健康的人后,也可能因此对他的人生有负面影响。
这个问题的重要性,最适合用条件机率的观点来解释。
设人群中有1%的人罹患此疾病,而其他人是健康的。我们随机选出任一个体,并将患病以disease、健康以well表示:
P(disease) = 1% = 0.01 andP(well) = 99% = 0.99. 假设检验动作实施在未患病的人身上时,有1%的机率其结果为假阳性(阳性以positive表示)。意即:
P(positive | well) = 1%,而且P(negative | well) = 99%. 最后,假设检验动作实施在患病的人身上时,有1%的机率其结果为假阴性(阴性以negative表示)。意即:
P(negative | disease) = 1%且P(positive | disease) = 99%。 现在,由计算可知:
是整群人中健康、且测定为阴性者的比率。
是整群人中得病、且测定为阳性者的比率。
是整群人中被测定为假阳性者的比率。
是整群人中被测定为假阴性者的比率。
进一步得出:
是整群人中被测出为阳性者的比率。
是某人被测出为阳性时,实际上真的得了病的机率。
这个例子里面,我们很轻易可以看出 P(positive|disease)=99% 与 P(disease|positive)=50% 的差距:前者是你得了病,而被检出为阳性的条件机率;后者是你被检出为阳性,而你实际上真得了病的条件机率。由我们在本例中所选的数字,最终结果可能令人难以接受:被测定为阳性者,其中的半数实际上是假阳性。
离散概率分布:均匀・伯努利・几何・ 二项 ・泊松・ 超几何 ・ 多项 ・ 负二项 ・玻尔兹曼・ 复合泊松 ・退化・ 高斯-库兹明 ・对数・ 拉德马赫 ・ Skellam
Yule-Simon ・ζ・齐夫・ 齐夫-曼德尔布罗特 ・ 抛物线分形
连续概率分布:均匀 ・ 正态 ・指数・ β(贝塔) ・ β'(第二类) ・柯西・ χ2(卡方) ・ δ(德尔塔) ・Erlang・ 广义误差 ・F・衰落・ Fisher的z
Fisher-Tippett ・ γ(伽玛) ・ 广义极值 ・ 广义双曲 ・ 半逻辑 ・ Hotelling的T平方 ・ 双曲正割 ・ 超指数 ・ 逆χ2 ・ 逆高斯 ・ 广义逆高斯
逆γ ・ Kumaraswamy ・Landau・拉普拉斯・列维・稳定・逻辑・ 对数正态・麦克斯韦-玻尔兹曼・麦克斯韦速率分布律・ 玻色-爱因斯坦
费米-狄拉克 ・ Pareto ・Pearson・ 极角 ・ 余弦平方 ・瑞利・ 相对论的Breit-Wigner ・莱斯・t(学生氏) ・三角・ 第一类Gumbel
第二类Gumbel ・ Voigt ・ von Mises ・ 韦氏 ・ Wigner半圆形
其它分布:康托尔分布 ・ 条件概率 ・ 指数分布族 ・ infinitely divisible ・ location-scale family ・ marginal ・ maximum entropy ・ phase-type ・ posterior
prior ・ 拟概率 ・抽样分配・singular
多随机变量:狄利克雷・肯特・矩阵常态分配・ 多变量常态分配 ・ von Mises-Fisher ・ Wigner拟概率 ・ Wishart Ewens抽样公式
 爱华网
爱华网