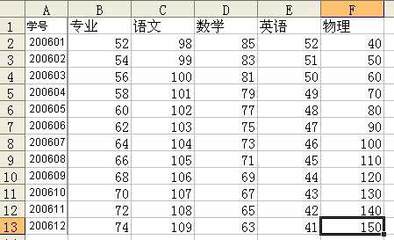
初等函数是由幂函数(power function)、指数函数(exponential function)、对数函数(logarithmicfunction)、三角函数(trigonometric function)、反三角函数(inverse trigonometic function)与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方)及有限次函数复合所产生、并且能用一个解析式表示的函数。它是最常用的一类函数,包括常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数(以上是基本初等函数),以及由这些函数经过有限次四则运算或函数的复合而得的所有函数。即基本初等函数经过有限次的四则运算或有限次的函数复合所构成并可以用一个解释式表出的函数,称为初等函数。
初等函数_初等函数 -概念
初等函数是由幂函数(powerfunction)、指数函数(exponentialfunction)、对数函数(logarithmicfunction)、三角函数(trigonometricfunction)、反三角函数(inversetrigonometicfunction)与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方)及有限次函数复合所产生、并且能用一个解析式表示的函数。
它是最常用的一类函数,包括常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数(以上是基本初等函数),以及由这些函数经过有限次四则运算或函数的复合而得的所有函数。即基本初等函数经过有限次的四则运算或有限次的函数复合所构成并可以用一个解释式表出的函数,称为初等函数。
还有一系列双曲函数也是初等函数,如sinh的名称是双曲线正弦或超正弦,cosh是双曲余弦或超余弦,tanh是双曲线正切、coth是双曲线余切、sech是双曲线正割、csch是双曲线余割。初等函数在其定义区间内连续。
初等函数_初等函数 -实例介绍
常值函数
对定义域中的一切x对应的函数值都取某个固定常数的函数。
指数函数
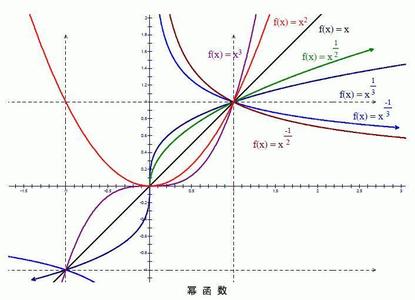
幂函数
形如y=x^a的函数,式中a为实常数。
指数函数
形如y=a^x的函数,式中a为不等于1的正常数。
基本函数
对数函数
指数函数的反函数,记作y=logaax,式中a为不等于1的正常数,定义域是X〉0。指数函数与对数函数之间成立关系式,logaax=x。
三角函数
即正弦函数y=sinx,余弦函数y=cosx,正切函数y=tanx,余切函数y=cotx,正割函数y=secx,余割函数y=cscx(见三角学)。
反三角函数
三角函数的反函数――反正弦函数y=arcsinx,反余弦函数y=arccosx(-1≤x≤1,0≤y≤π),反正切函数y=arctanx,反余切函数y=arccotx(-∞<+∞,θ<π等="等"以上这些函数常统称为基本初等函数="以上这些函数常统称为基本初等函数">
双曲正弦或超正弦sinhx=(e^x-e^(-x))/2
双曲余弦或超余弦coshx=(e^x+e^(-x))/2
双曲正切tanhx=sinhx/coshx
双曲余切cothx=1/tanhx
双曲正割sechx=1/coshx
双曲余割cschx=1/sinhx
一个初等函数,除了可以用初等解析式表示以外,往往还有其他表示形式,例如,三角函数y=sinx可以用无穷级数表为初等函数可以按照解析表达式分类为:初等函数是最先被研究的一类函数,它与人类的生产和生活密切相关,并且应用广泛。为了方便,人们编制了各种函数表,如平方表、开方表、对数表、三角函数表等。
初等函数_初等函数 -正文
 爱华网
爱华网