等腰直角三角形是一种特殊的三角形,具有所有三角形的性质:稳定性,两直角边相等直角边夹亦直角锐角45,斜边上中线角平分线垂线三线合一,等腰直角三角形斜边上的高为外接圆的半径R,那么设内切圆的半径r为1,则外接圆的半径R就为(根号2加1),所以r:R=1:(根号2加1)。等腰直角三角形中的四条特殊的线段:角平分线,中线,高,中位线。
等腰直角三角形_等腰直角三角形 -概念
等腰直角三角形是一种特殊的三角形。具有所有三角形的性质:稳定性 。
两直角边相等 直角边夹亦直角锐角45° 。
斜边上中线角平分线垂线 三线合一。
等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径(因为等腰直角三角形的两个小角均为45度,高又垂直于斜边,所以两个小三角形均为等腰直角三角形,则两腰相等);那么设内切圆的半径r为1,则外接圆的半径R就为(根号2加1),所以r:R=1:(根号2加1)。
等腰直角三角形_等腰直角三角形 -关系
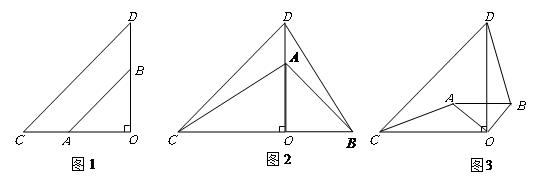
等腰直角三角形的边角之间的关系 :
(1)三角形三内角和等于180°;
(2)三角形的一个外角等于和它不相邻的两个内角之和;
(3)三角形的一个外角大于任何一个和它不相邻的内角;
4)三角形两边之和大于第三边,两边之差小于第三边;
(5)在同一个三角形内,大边对大角,大角对大边.
等腰直角三角形中
的四条特殊的线段:角平分线,中线,高,中位线.(1)三角形的角平分线的交点叫做三角形的内心,它是三角形内切圆的圆心,它到各边的距离相等.
(三角形的外接圆圆心,即外心,是三角形三边的垂直平分线的交点,它到三个顶点的距离相等).
(2)三角形的三条中线的交点叫三角形的重心,它到每个顶点的距离等于它到对边中点的距离的2倍。
(3)三角形的三条高的交点叫做三角形的垂心。
(4)三角形的中位线平行于第三边且等于第三边的二分之一。
注意!
①三角形的内心、重心都在三角形的内部 .②钝角三角形垂心、外心在三角形外部。③直角三角形垂心、外心在三角形的边上。(直角三角形的垂心为直角顶点,外心为斜边
中点。)④锐角三角形垂心、外心在三角形内部。
等腰直角三角形_等腰直角三角形 -线段
中线:顶点与对边中点的连线,平分三角形。高:顶点到对边垂足的连线。
角平分线;顶点到两边距离相等的点所构成的直线。
中位线:任意两边中点的连线。
等腰直角三角形_等腰直角三角形 -性质
等边三角形的性质:(具有等腰三角形的所有性质,结合定义更特殊)1)等边三角形的内角都相等,且为60度 。
2)等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一) 。
3)等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或所对角的平分线所在直线 。
等边三角形的判定:(首先考虑判断三角形是等腰三角形)
(1)三边相等的三角形是等边三角形(定义)
2)三个内角都相等的三角形是等边三角形
3)有一个角是60度的等腰三角形是等边三角形
理解等边三角形的性质与判定。
首先明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
推论1:三个角都相等的三角形是等边三角形
推论2:有一个角等于60°的等腰三角形是等边三角形
等边三角形重心、内心 、外心、垂心重合,称为等边三角形的中心。
等边三角形的中心、内心和垂心重合于一点。(三心合一)
等边三角形的每条边上的中线、高或对角平分线重合。(三线合一)
等边三角形的复数性质
A,B,C三点的复数构成正三角形
等价于 A+wB+wwC=0
其中
w=cos(2π/3)+isin(2π/3)
1+w+ww=0
等腰直角三角形_等腰直角三角形 -生活中的三角形物品
雨伞、帽子、彩旗、灯罩、风帆、小亭子、雪山、楼顶、切成三角形的西瓜、火炬冰淇淋、热带鱼的边缘线、蝴蝶翅膀、火箭、竹笋、宝塔、金字塔、三角内裤、机器上用的三角铁、某些路标、长江三角洲、斜拉桥等。等腰直角三角形_等腰直角三角形 -解三角形
在三角形ABC中,角A,B,C的对边分别为a,b,c. 则有(1)正弦定理
a/SinA=b/SinB= c/SinC=2r (外接圆半径为r)
(2)余弦定理。
a^2=b^2+c^2-2bc*CosA cosA=c^2+b^2-a^2/2cb
b^2=a^2+c^2-2ac*CosB cosB=a^2+c^2-b^2/2ac
c^2=a^2+b^2-2ab*CosC cosC=a^2+b^2-c^2/2ab
等腰直角三角形_等腰直角三角形 -勾股定理
在Rt三角形ABC中,〈A=90度,则AB・AB+AC・AC=BC・BC
A>90度,则
AB・AB+AC・AC>BC・BC
等腰直角三角形_等腰直角三角形 -三角形相关定理
重心定理
三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍.上述交点叫做三角形的重心.
外心定理
三角形的三边的垂直平分线交于一点.这点叫做三角形的外心.
垂心定理
三角形的三条高交于一点.这点叫做三角形的垂心.
内心定理
三角形的三内角平分线交于一点.这点叫做三角形的内心.
旁心定理
三角形一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.
三角形的重心、外心、垂心、内心、旁心称为三角形的五心.
它们都是三角形的重要相关点.
中位线定理
三角形的中位线平行于第三边且等于第三边的一半.三边关系定理
三角形任意两边之和大于第三边,任意两边之差小于第三边.
三角形面积计算公式
S(面积)=a(边长)h(高)/2---三角形面积等于一边与这边上的高的积的一半
等腰直角三角形_等腰直角三角形 -梅涅劳斯定理
人物
梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。证明:
过点A作AG∥BC交DF的延长线于G,
则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1
它的逆定理也成立:若有三点F、D、E分别在的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。利用这个逆定理,可以判断三点共线。
说明
另外,有很多人会觉得书写这个公式十分烦琐,不看书根本记不住,下面从别人转来一些方法帮助书写
为了说明问题,并给大家一个深刻印象,我们假定图中的A、B、C、D、E、F是六个旅游景点,各景点之间有公路相连。我们乘直升机飞到这些景点的上空,然后选择其中的任意一个景点降落。我们换乘汽车沿公路去每一个景点游玩,最后回到出发点,直升机就停在那里等待我们回去。
我们不必考虑怎样走路程最短,只要求必须“游历”了所有的景点。只“路过”而不停留观赏的景点,不能算是“游历”。
例如直升机降落在A点,我们从A点出发,“游历”了其它五个字母所代表的景点后,最终还要回到出发点A。
另外还有一个要求,就是同一直线上的三个景点,必须连续游过之后,才能变更到其它直线上的景点。
从A点出发的旅游方案共有四种,下面逐一说明:
方案 ① ――从A经过B(不停留)到F(停留),再返回B(停留),再到D(停留),之后经过B(不停留)到C(停留),再到E(停留),最后从E经过C(不停留)回到出发点A。
按照这个方案,可以写出关系式:
(AF:FB)*(BD:DC)*(CE:EA)=1。
现在,您知道应该怎样写“梅涅劳斯定理”的公式了吧。
从A点出发的旅游方案还有:
方案 ② ――可以简记为:A→B→F→D→E→C→A,由此可写出以下公式:
(AB:BF)*(FD:DE)*(EC:CA)=1。从A出发还可以向“C”方向走,于是有:
方案 ③ ―― A→C→E→D→F→B→A,由此可写出公式:
(AC:CE)*(ED:DF)*(FB:BA)=1。 从A出发还有最后一个方案:
方案 ④ ―― A→E→C→D→B→F→A,由此写出公式:
(AE:EC)*(CD:DB)*(BF:FA)=1。
我们的直升机还可以选择在B、C、D、E、F任一点降落,因此就有了图中的另外一些公式。
值得注意的是,有些公式中包含了四项因式,而不是“梅涅劳斯定理”中的三项。当直升机降落在B点时,就会有四项因式。而在C点和F点,既会有三项的公式,也会有四项的公式。公式为四项时,有的景点会游览了两次。
不知道梅涅劳斯当年是否也是这样想的,只是列出了一两个典型的公式给我们看看。
现在是否可以说,我们对梅涅劳斯定理有了更深刻的了解呢。那些复杂的相除相乘的关系式,不会再写错或是记不住吧。
等腰直角三角形_等腰直角三角形 -面积公式
S=(1/2)*底*高
S=(1/2)*a*b*sinC(C为a,b的夹角)
S=底*高/2
底X高除2二分之一的(两边的长度X夹角的正弦)
s=1/2的周长*内切圆半径
两边之和大于第三边,两边之差小于第三边
大角对大边
周长c=三边之和a+b+c
面积
s=1/2ah(底*高/2)
s=1/2absinC(两边与夹角正弦乘积的一半)
s=1/2acsinB
s=1/2bcsinA
s=根号下:p(p-a)(p-b)(p-c)其中p=1/2(a+b+c)
这个公式叫海伦公式
正弦定理:
sinA/a=sinB/b=sinc/C
余弦定理:
a^2=b^2+c^2-2bccosA
b^2=a^2+c^2-2accosB
c^2=a^2+b^2-2abcosA
三角形2条边向加大于第三边.
三角形面积=底*高/2
三角形内角和=180度
求面积吗(上底+下底)×高÷2
三角形面积=底*高/2
三角形面积公式:
底*高/2
三角形的内角和是180度
等腰直角三角形_等腰直角三角形 -证明方法
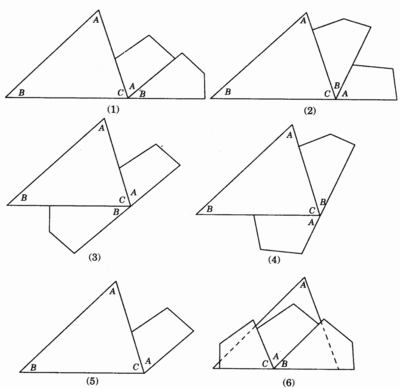
证法1
作四个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c.把它们拼成如图那样的一个多边形,使D、E、F在一条直线上.过点C作AC的延长线交DF于点P.∵D、E、F在一条直线上,且RtΔGEF≌RtΔEBD,
∴∠EGF=∠BED,
∵∠EGF+∠GEF=90°,
∴∠BED+∠GEF=90°,
∴∠BEG=180°
 爱华网
爱华网