通径分析可用于分析多个自变量与应变量之间的线性关系,是回归分析的拓展,可以处理较为复杂的变量关系。可用于分析多个自变量与应变量之间的线性关系,是回归分析的拓展,可以处理较为复杂的变量关系。通径分析中受到模型中某些变量影响的变量称为 内生变量,如图1中的D,通径图中有朝内的箭头指向它们。通径分析中只受到模型之外的其他因素影响的变量称为外生变量,如图1中的A、B、C、е,通径图中没有箭头指向它们。它是一个不带单位的相对数,因而又具有 相关系数的性质,是具有方向性的相关系数,能表示原因与结果( 自变量与依变量)之间的关系,它是介于 回归系数和相关系数之间的一种 统计量,可用于各种性状间的 相关分析。
通径分析_通径分析 -简介
如当 自变量数目比较多,且自变量间相互关系比较复杂(如:有些自变量间的关系是相关关系,有些自变量间则可能是因果关系)或者某些自变量是通过其他的自变量间接地对应变量产生影响,这时可以采用通径分析。
通径分析_通径分析 -基本概念
2.1 通径模型(path model):
通径模型是由一组线性方程组成的,反映 自变量、中间变量、 潜变量和应变量之间相互关系的模型,是以多元线性回归方程为基础的模型。
2.2 通径图(path graph):
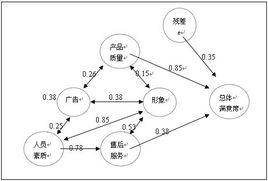
通径图(如图1)可以直观的表现各个变量之间的相互关系。通径图中的单箭头线称为直接通径(如A到D),简称通径(path),表示因果关系,方向由原因指向结果。双箭头线称为相关线(correlation line),表示变量间互为因果,是平行关系(如A与B)。
A B C
D
е
图1 通径图
其中е为 误差项。
2.3 外生变量和 内生变量:
通径分析中只受到模型之外的其他因素影响的变量称为外生变量,如图1中的A、B、C、е,通径图中没有箭头指向它们。外生变量之间如果有相关关系,则用双箭头线表示。
通径分析中受到模型中某些变量影响的变量称为 内生变量,如图1中的D,通径图中有朝内的箭头指向它们。
2.4 通径系数(path coefficient):
通径系数是是用来表示相关变量因果关系的 统计量,是标准化的 偏回归系数 ,也称作通径权重。 通径系数一般用 最小二乘法法(OLS)或极大似然估计法(MLE) 来估计?
2.4.1 通径系数的数学表达式
如果我们估计的 线性回归方程为:
= + + (1)
或
= + + + ( 为 残差)(2)
由于 和 带有量纲,我们不能通过 、 来比较 对 的影响大小。如果要比较 和 对 的影响,需要消除量纲的影响,需要将 、 及 标准化。
由 = + + + 可得:
= + + (3)
公式(2)与公式(3)相减得:
- = - )+ ( - )+ (4)
公式(4)可变换为下式:
= ・ + ・ + ・ (5)
公式(5)中 、 、 、 分别表示 、 及 的标准差。 和 分别为 自变量 、 的标准化 偏回归系数。 为除了 自变量以外的其他因素对应变量 的影响大小。如果我们以 、 、和 分别表示 、 和 到 的 通径系数,那么:
= , = , =
当我们估计的 线性回归方程有多个 自变量,且自变量间两两相关时,各自变量及 残差到应变量的 通径系数的 数学表达式同上。
2.4.2 通径系数的性质:
(1) 通径系数具有 偏回归系数的性质。它是变量标准化后的 偏回归系数,能够表示变量间的因果关系,故仍具有偏回归系数的性质。
(2) 通径系数具有 相关系数的性质。它是一个不带单位的相对数,因而又具有 相关系数的性质,是具有方向性的相关系数,能表示原因与结果( 自变量与依变量)之间的关系,它是介于 回归系数和相关系数之间的一种 统计量,可用于各种性状间的 相关分析。
(3) 通径系数是一个不带单位的相对数。可以用它来估计自变量对应变量直接影响效应的大小,比较其相对重要性。
(4)利用 通径系数分析,可以帮助我们建立“最优”多元 回归方程。
2.5 决定系数(Determination coefficient)
通径系数的平方称为 决定系数,表示自变量或 误差能够解释应变量总 变异的程度。
3 通径分析的显着性检验
通径分析的 显着性检验包括以下四项:
(1) 回归方程显着性检验:采用F检验法;
(2) 通径系数显着性检验:采用F检验法或T检验法;
(3) 通径系数差异显着性检验:采用F检验法或T检验法;
(4) 两次通径分析相应通径系数显着性检验:采用F检验法或t检验法。
一般情况下,第(3)种检验和第(4)种检验在一般的 多元线性回归分析中无法实现,因为不同 偏回归系数带有不同 量纲,但是在通径分析中,这两种检验可以实现。
 爱华网
爱华网