土压力 (earth pressure ):建筑学术语,指土体作用在建筑物或构筑物上的力,促使建筑物或构筑物移动的土体推力称主动土压力;阻止建筑物或构筑物移动的土体对抗力称被动土压力。朗肯和库伦土压力理论都是建立在某些人为假定的基础上,朗肯假定墙背为理想的光滑面,忽略了墙与土之间的摩擦对土压力的影响,库伦理论虽计及墙背与填土的摩擦作用,但却假定土中的滑裂面是通过墙锺的平面,与比较严格的挡土墙土压力解(按极限平衡理论,考虑d,土体内的滑裂面是由一段平面和一段对数螺线曲面所组成的复合滑动面求得),计算结果都有一定的误差。
静止土压力系数_土压力 -静止压力
挡土墙完全没有侧向位移、偏转和自身弯曲变形时,作用在其上的土压力即为静止土压力,此时墙后土体处于侧限应力状态(弹性平衡状态),与土的自重应力状态相同。 半无限土体中z深度处一点的应力状态,巳知其水于面和竖直面都是主应力面。作用于该土单元上的竖直向主应力就是自重应力σv=γz,则水平向自重应力(静止土压力强度): σ= σ=kγz
图1 静止土压力分布
式中――k土的侧压力系数或静止土压力系数,对于正常固结粘性土,可近似按k≈1-sin j’(Jaky,1944),(j’为土的有效内摩擦角)。
γ ――墙后填土重度。
静止土压力强度分布沿墙高呈三角形分布。若墙高为H,则作用于单位长度墙上的总静止土压力Eo为 :Eo的作用点应在墙高的1/3处。
静止土压力系数_土压力 -库伦压力
计算理论
库伦土压力理论是根据墙后土体处于极限平衡状态并形成一滑动楔体时,从楔体的静力平衡条件得出的土压力计算理论。
基本假设 :
① 墙后的填土是理想的散粒体(粘聚力c=0);
② 墙背倾斜、粗糙、墙后填土面倾斜;
③ 滑动破坏面为一平面(墙背AB和土体内滑动面BC);
④ 刚体滑动。不考虑滑动楔体内部的应力和变形条件;
⑤ 楔体ABC整体处于极限平衡状态。在AB和BC滑动面上,抗剪强度均巳充分发挥。即剪应力τ均已达抗剪强度τ。
图2 柔性挡土墙的土压力
图3 刚性挡土墙的土压力
主动计算
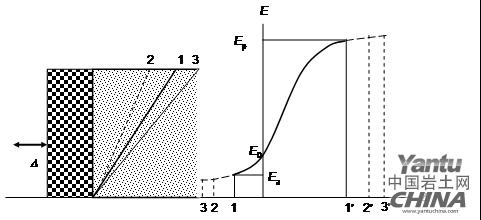
图3一刚性挡土墙,墙高为H,墙背AB的倾斜角为α,填土顶面坡度为β,填料为砂土,其单位重为γ,内摩擦角为ψ,墙背摩擦角为δ。若墙背AB在土压力作用下向左移动,使土体的侧压力减小而发生破坏,破坏时产生一个处于极限平衡状态的滑动土楔体ABC,此时墙背所受的土压力称为主动土压力E(图a)。反之,如果墙背AB在外力作用下向右移动,并使土体的侧压力增大而发生破坏,也产生一个处于极限平衡状态的滑动土楔体ABC,而墙背所受的土压力称为被动土压力E(图b)。如图上所示,被动土压力大于主动土压力。土体破裂面BC一般呈曲线状。为了简化计算,C.-A.de库仑假设破裂面为直线,并据此导出下列计算土压力公式:
土压力
式中γ为土的容量;Ka和Kp分别为主动土压力系数和被动土压力系数:
土压力
如果墙壁垂直且光滑,填土表面为水平,即α=90°,β=δ=0,式(3)、(4)变为:
土压力
这种情况称为兰金状态。上述库仑和兰金理论均假定土压力的分布规律为三角形,其合力作用点在墙背高度的1/3处。
苏联B. B. 索科洛夫斯基用极限平衡理论求出具有任何填土表面的倾斜挡土墙土压力的精确解答,他求得的滑动破裂线都是对数螺旋曲线。对于墙后有水平填土表面的垂直刚性挡土墙,用库仑和兰金理论所得的结果与索科洛夫斯基的精确解答大致有如下关系:
E=1.24E,
E=0.98E,
式中E为按兰金理论计算的结果;E为按库仑理论计算的结果;E为按精确方法计算的结果。由此可知,确定挡土墙主动土压力时,用库仑理论能得出足够精确的结果。但据一些学者的实验研究,用库仑理论确定被动土压力,误差较大,而且这个误差还随着土的内摩擦角的增大而增大。
静止土压力系数_土压力 -朗肯压力
依据
朗肯土压力理论是根据半空间体的应力状态和土的极限平衡理论得出的土压力计算理论之一。
基本假设:墙背直立、光滑,墙后填土面水平。 这时,墙背与填土界面上的剪应力为零。不改变右边土体中的应力状态。当挡土墙的变位符合上述主动或被动极限平衡条件时,作用在挡土墙墙背上的土压力即为朗肯主动土压力或朗肯被动土压力。
计算
(1)主动土压力计算
土的极限平衡条件:土体处于极限平衡状态时土的应力状态和土的抗剪强度指标之间的关系式。
大主应力σ = σ=γz
小主应力σ = σ
主动土压力强度σ = σ
粘性土
无粘性土
主动土压力系数
粘性土的主动土压力强度包括两部分:
1.由土自重引起的土压力γzKa;
2.由粘聚力c引起的负侧压力2cKa1/2。
其中负侧压力对增背是拉应力,实际上墙与土在很小的拉力作用下就会分离(一般情况下认为土不能承受拉应力),故在计算土压力时,这部分应忽去不计。
临界深度z
粘性土主动土压力作用点位于墙底以上(H - z)/3处
无粘性土主动土压力,E― 合力(集中力),作用点位于墙底以上H /3处
(2)被动土压力计算
土的极限平衡条件
大主应力σ = σ
小主应力σ = σ=γz
被动土压力强度σ = σ
粘性土
无粘性土
被动土压力系数
粘性土被动土压力
E方向垂直墙背,作用点位于梯形面积的重心上
非粘性土被动土压力
E方向垂直墙背,作用点位于作用点位于墙底以上H /3处
静止土压力系数_土压力 -比较
一、朗肯与库伦土压力理论均属于极限状态土压力理论。用这两种理论计算出的土压力都是墙后土体处于极限平衡状态下的主动与被动土压力。
二、两种分析方法上存在的较大差别,主要表现在研究的出发点和途径的不同。朗肯理论是从研究土中一点的极限平衡应力状态出发,首先求出的是作用在土中竖直面上的土压力强度sa或sp及其分布形式,然后再计算出作用在墙背上的总土压力Ea和Ep,因而朗肯理论属于极限应力法。库伦理论则是根据墙背和滑裂面之间的土楔,整体处于极限平衡状态,用静力平衡条件,先求出作用在墙背上的总土压力Ea或Ep,需要时再算出土压力强度sa或sp及其分布形式,因而库伦理论属于滑动楔体法。
三、上述两种研究途径中,朗肯理论在理论上比较严密,但只能得到理想简单边界条件下的解答,在应用上受到限制。库伦理论显然是一种简化理论,但由于其能适用于较为复杂的各种实际边界条件,且在一定范围内能得出比较满意的结果,因而应用广泛。
四、朗肯理论的应用范围:墙背垂直、光滑、墙后填土面水平,即a= 0,b= 0,d= 0。无粘性土与粘性土均可用。库伦理论的应用范围:用于包括朗肯条件在内的各种倾斜墙背的陡墙,填土面不限,即a,b,d可以不为零或等于零,故较朗肯公式应用范围更广。数解法一般只用于无粘性土,图解法则对于无粘性土或粘性土均可方便应用。
五、计算误差
朗肯和库伦土压力理论都是建立在某些人为假定的基础上,朗肯假定墙背为理想的光滑面,忽略了墙与土之间的摩擦对土压力的影响,库伦理论虽计及墙背与填土的摩擦作用,但却假定土中的滑裂面是通过墙锺的平面,与比较严格的挡土墙土压力解(按极限平衡理论,考虑d,土体内的滑裂面是由一段平面和一段对数螺线曲面所组成的复合滑动面求得),计算结果都有一定的误差。
对于主动土压力计算,各种理论的差别都不大。朗肯土压力公式简单,且能建立起土体处于极限平衡状态时理论破裂面形状和概念。在具体实用中,要注意边界条件是否符合朗肯理论的规定,以免得到错误的结果。库伦理论可适用于比较广泛的边界条件,包括各种墙背倾角、填土面倾角和墙背与土的摩擦角等,在工程中应用更广。被动土压力的计算、当d和j较小时,这两种古典土压力理论尚可应用;而当d和j较大时,误差都很大,均不宜采用。
静止土压力系数_土压力 -其他计算
确定土压力还有图解分析法和图解法。图解分析法是用作图确定近似于滑动线的精确曲线,然后确定滑落棱体各部分的重量,借助力的三角形,求出土压力的数值。图解法是以库仑假设为基础,即假设滑动线为直线,此法一般仅适用于确定主动土压力,结果同精确解相近。确定被动土压力则必须采用图解分析法。图解法和图解分析法的优点在于能自行核对,避免较大误差,可以用简便的作图方法计算复杂条件下的土压力。
有地下水位时土压力的计算
地下水位对土压力的影响,具体表现在:
(1) 地下水位以下填土重量将因受到水的浮力而减小.计算土压力时应用浮容重γ;
(2) 地下水对填土的强度指标c、j的影响。一般认为对砂性土的影响可以忽略;但对粘性填土,地下水将使c、j值减小.从而使土压力增大;
(3) 地下水对墙背产生静水压力作用。
土压力
水土合算→粘性土
水土分算→无粘性土
连续均布荷载作用下土压力计算
地表连续均布荷作用下,作用在墙背面的土压力强度sa由两部分组成:一部分由均布荷载q引起(常数),其分布与深度z无关; 另一部分由土重引起,与深度z成正比。总土压力E即为梯形分布图的面积。
地表局部荷载作用下土压力计算
填土表面有局部荷载q作用下,则q对墙背产生的附加土压力强度值仍可用朗肯公式计算,即sa=qKa ,但其分布范围缺乏在理论上的严格分析。一种近似方法认为,地面局部荷载产生的土压力是沿平行于破裂面的方向传递至墙背上的。
墙背设置卸荷平台时土压力计算
为了减少作用在墙背上的主动土压力.有时采用在场背中部加设卸荷平台的办法。此时,平台以上Hl高度内,可按朗肯理论,计算作用在AB面上的土压力分布。由于平台以上土重W已由卸荷台BCD承担,故乎台下C点处土压力变为零,从而起到减少平台下H2段内土压力的作用。减压范围,一般认为至滑裂面与墙背交点E处为止。连接图中相应的C和E,则图中阴影部分即为减压后的土压力分布。显然卸荷平台伸出越长,则减压作用越大。
 爱华网
爱华网



