平面几何。几何学起源于土地测量,几千年来,人们对几何学进行了深入的研究,现已发展成为一门具有严密的逻辑体系的数学分支。人们从少量的公理出发,经过演绎推理得到不少结论,这些结论一般就称为定理。平面几何中有不少定理,除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础,可以推出不少几何事实,得到完美的结论,以至巧妙而简捷地解决不少问题。
几何学起源于土地测量,几千年来,人们对几何学进行了深入的研究,现已发展成为一门具有严密的逻辑体系的数学分支。人们从少量的公理出发,经过演绎推理得到不少结论,这些结论一般就称为定理。平面几何中有不少定理,除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础,可以推出不少几何事实,得到完美的结论,以至巧妙而简捷地解决不少问题。
立体几何定理_平面几何 -平面几何定义
立体几何定理_平面几何 -平面几何著名定理
梅内劳斯定理
亚历山大里亚的梅内劳斯(Menelaus,约公元100年,他和斯巴达的Menelaus是两个人)曾著《球面论》,着重讨论球面三角形的几何性质.以他的名子命名的“梅内劳斯定理”现载在初等几何和射影几何的书中,是证明点共线的重要定理.
定理 一直线与△ABC的三边AB,BC,CA或延长线分别相交于X,Y,Z,则
平面几何
塞瓦定理
意大利数学家塞瓦(G.Ceva)在1678年发表了下面的十分有用的定理,它是证明共点线的重要定理.
定理 在△ABC内任取一点P,直线AP,BP,CP分别与边BC,CA,AB相交于D,E,F,则
平面几何
斯台沃特定理
定理 △ABC的边BC上任取一点D,若BD=u,DC=v,AD=t,则
平面几何
托勒密定理
托勒密(Ptolemy,约公元85~165年)是古代天文学的集大成者.一般几何教科书中的“托勒密定理”(圆内接四边形的对边积之和等于对角线之积),实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质。
定理 如果四边形内接于圆,那么它的两对对边的乘积之和等于它的对角线的乘积.
斯泰纳-莱默斯定理
西姆松定理
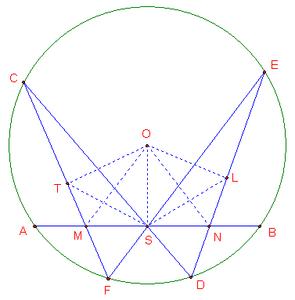
蝴蝶定理
莫莱定理
立体几何定理_平面几何 -平面几何与立体几何的相似命题
1, 平面中,周长相等的正三角形,正方形,圆的面积为 , , ,则 < < ;空间中,全面积相等的正四面体,正方体,球的体积为 , , ,则 < < 。这两个命题中,周长在空间中对应全面积,正三角形对应正四面体,正方形对应正方体,圆对应球体。换言之,平面中,周长一定时,越接近圆形的图形面积最大;空间中,全面积一定时,越接近球形的空间图形,体积越大。2,平面中,面积相等的正三角形,正方形,圆的周长为 , , ,则 > > 空间中,体积相等的正四面体,正方体,球的表面积为 , , ,则 > > 。换言之,平面中,面积一定时,越接近圆的图形周长最小;空间中,体积一定时,越接近球的空间图形,表面积越小。这也反映了宇宙中星体为什么大多以球体或接近球体的形式存在,因为球体的表面积最小,表面积越小越稳定;动物世界中,弱小动物遇到敌人时,缩成一团,是出于本能,将受攻击的区域减少到最小,因为球形的表面积最小。
3, 平面中,不共线的三点可确定一个圆;空间中,不共面的四点可确定一个球。
4, 平面中,过平面外一点有且只有一条直线与已知直线平行;空间中,过平面外的一条平行直线有且只有一个平面与已知平面平行。
5, 平面中,过一点有且只有一条直线与已知直线垂直;空间中,过一条直线有且只有一个平面与已知平面垂直。 6,平面中的勾股定理也可推广到空间:(1)长方体的体对角线长的平方等于共顶点的三条棱长的平方和;(2)设三棱锥A―BCD的三个侧面两两互相垂直,则有等式 + + = 恒成立。
7,平面中,等边ΔABC内任一点到各边的距离之和为定值(等边ΔABC的高);等腰ΔABC底边上任一点到两腰的距离之和为定值(一腰上的高)。空间中,正四面体内任一点到各面的距离之和为定值(正四面体的高);正三棱锥底面上任一点到各侧面的距离之和为定值(一侧面上的高)。
8,圆的周长公式: ;球的表面积公式: ;圆的面积公式: ;球的体积公式: 。其中R表示半径,的指数1,2以及系数 与维数之间存在着一种对应。因为平面是二维的,空间是三维的。
9,平面中,三角形被平行于它一边的直线所截得的三角形与原三角形的面积的比等于对应边的平方比;空间中,棱锥被平行于它低面的平面所截得的小棱锥与原棱锥的体积的比等于对应边的立方比。
10,平面中,三角形的面积公式: ;空间中有两个相似命题:(1)棱锥的体积公式; 。其中, 分别表示三角形的边,棱锥的低面积, 表示高。(2)三棱锥的体积也可按此公式计算: ,其中, 为三棱锥一个侧面的面积, 为该侧面与所对的侧棱间的距离。
11,平面中,梯形的面积公式: ;空间中,低面是梯形的直棱住的体积公式: ,其中, 表示两个平行侧面的面积, 表示这两个侧面间的距离。
 爱华网
爱华网


