如果对于函数f(x)的定义域内任意一个x,都有f(-x)= - f(x),那么函数f(x)就叫做奇函数(odd function)。奇函数的定义域必须关于原点(0,0)对称,否则不能成为奇函数。设f(x)在I上可导,若f(x)在I上为奇函数,则f'(x)在I上为偶函数。当且仅当f(x)=0(定义域关于原点对称)时,f(x)既是奇函数又是偶函数。
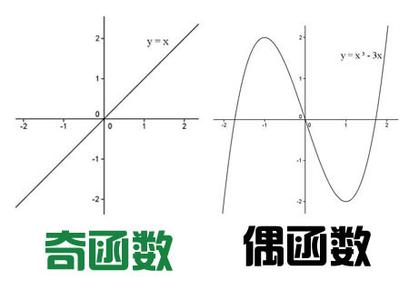
奇函数加奇函数_奇函数 -函数定义
奇函数2、奇函数图象关于原点(0,0)中心对称。
3、奇函数的定义域必须关于原点(0,0)对称,否则不能成为奇函数。
4、若F(X)为奇函数,定义域中含有0,则F(0)=0.1、在奇函数f(x)中,f(x)和f(-x)的符号相反且绝对值相等,即f(-x)=-f(x),反之,满足f(-x)=-f(x)的函数y=f(x)一定是奇函数。例如:f(x)=x^(2n-1),n∈Z;(f(x)等于x的2n-1次方,n属于整数)
2、奇函数图象关于原点(0,0)中心对称。
3、奇函数的定义域必须关于原点(0,0)对称,否则不能成为奇函数。
4、若F(X)为奇函数,定义域中含有0,则F(0)=0
相关函数:偶函数,非奇非偶函数
5、设f(x)在I上可导,若f(x)在I上为奇函数,则f'(x)在I上为偶函数。
即f(x)=-f(-x)对其求导f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)偶函数与奇函数满足下列基本性质
奇函数加奇函数_奇函数 -运算法则
(1) 两个偶函数相加所得的和为偶函数。(2) 两个奇函数相加所得的和为奇函数。(3) 一个偶函数与一个奇函数相加所得的和为非奇非偶函数。(4) 两个偶函数相乘所得的积为偶函数。(5) 两个奇函数相乘所得的积为偶函数。(6) 一个偶函数与一个奇函数相乘所得的积为奇函数。(7) 若f(x)为奇函数,且f(x)在x=0时有定义,那么一定有f(0)=0。(8) 定义在R上的奇函数f(x)必定满足f(0)=0。(9) 当且仅当f(x)=0(定义域关于原点对称)时,f(x)既是奇函数又是偶函数。(10) 奇函数在对称区间上的积分为零。奇函数加奇函数_奇函数 -函数图像
奇偶函数(1) 奇函数的图象关于原点中心对称。(2) 偶函数的图象关于Y轴对称。(3) 奇、偶函数的定义域一定关于原点对称。(4) 奇函数的偶次项系数等于0,偶函数的奇次项系数等于0。(5) Y=0即是X轴,既是奇函数也是偶函数。
奇函数加奇函数_奇函数 -函数例子
奇函数:F(X)=-F(-X),当在x=0处有定义时,有F(0)=0。常见的奇函数有F(X)=sinX。偶函数图象关于Y轴对称,F(x)=F(-X),如F(X)=cosX。对于函数y=ax^2+bx+c(a,b,c∈R),当a=0,b=0,c=0时,f(x)既是奇函数又是偶函数,当b∈R,a=0,c=0时,f(x)是奇函数;当a∈实数R,b=0,c∈实数R时,f(x)是偶函数。 爱华网
爱华网


