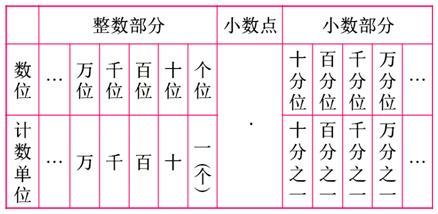
小数由整数部分、小数部分和小数点组成。当测量物体时往往会得到的不是整数的数,古人就发明了小数来补充整数小数是十进分数的一种特殊表现形式。分母是10、100、1000……的分数可以用小数表示。所有分数都可以表示成小数,小数中除无限不循环小数外都可以表示成分数。无理数为无限不循环小数。
小数_小数 -定义
把分母是10、100、1000......的分数改写成不带分母形式的数,叫做小数.
根据十进制的位值原则,把十进分数仿照整数的写法写成不带分母的形式,这样的数叫做小数.小数中的圆点叫做小数点,它是一个小数的整数部分和小数部分的分界号,小数点左边的部分是整数部分,小数点右边的部分是小数部分.整数部分是零的小数叫做纯小数,整数部分不是零的小数叫做带小数.例如0.3是纯小数,3.1是带小数.
要了解小数的意义,可从分数的意义着手,分数的意义可从子分割及合成活动来解释,当一个整体(指基准量)被等分后,在集聚其中一部份的量称为「分量」,而「分数」就是用来表示或纪录这个「分量」。例如:2/5是指一个整数被分成五等分后,集聚其中二分的「分量」。当整体被分成十等分、百等分、千等分……等时,此时的分量,就使用另外一种纪录的方法-小数。例如1/10记成0.1、2/100记成0.02、5/1000记成0.005……等。其中的「.」称之为小数点,用以分隔整数部分与无法构成整数的小数部分。整数非0者称为带小数,若为0则称纯小数。由此可知,小数的意义是分数意义的一环。
小数的读法有两种:一种是按照分数的读法来读.带小数的整数部分按整数读法读;小数部分按分数读法读.例如:0.38读作百分之三十八,14.56读作十四又百分之五十六.另一种读法,整数部分仍按整数的读法来读,小数点读作“点”,小数部分顺次读出每个数位上的数字.例如:0.45读作零点四五;56.032读作五十六点零三二.
小数大小的比较方法与整数基本相同,即从高位起,依次把相同数位上的数加以比较.
因此,比较两个小数的大小,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大;
因为小数是十进分数,所以有下列性质:①在小数的末尾添上零或去掉零,小数的大小
不变.例如;2.4=2.400,0.060=0.06.②小数点移动会引起小数大小发生变化.把小数点分别向右移动一位、二位、三位…位,则小数的值分别扩大10倍、100倍、1000倍……例如:把7.4扩大10倍是74,扩大100倍是740……
如果把小数点分别向左移动一位、二位、三位…则小数的值分别缩小到原来的十分之一、百分之一、千分之一….例如:把7.4缩小到原来的十分之一是0.74,缩小到原来的百分之一是0.074……
保留小数:按要求在舍去部分最高位进行四舍五入运算。
无限不循环小数只能用小数表示不能用分数表示,而所有的有限小数和无限循环小数均能用分数表示,小数分为有限小数和无限小数,有限小数如1/5,无限小数包括无限不循环小数(如0.010010001……)和无限循环小数(如1/3)
有理数(rationalnumber):能精确地表示为两个整数之比的数.
如3,-98.11,5.72727272……,7/22都是有理数.
整数和通常所说的分数都是有理数.有理数还可以划分为正有理数,0和负有理数.
在数的十进制小数表示系统中,有理数就是可表示为有限小数或无限循环小数的数.这一定义在其他进位制下(如二进制)也适用.《中国大百科全书》(数学))
因此,不矛盾。
小数乘以整数:
把小数乘法转化成整数乘法计算。
先把小数扩大成整数,按照整数乘法去计算,因数扩大了多少倍,积就要缩小多少倍。
积的小数位数与被乘数的小数位数有关,被乘数有几位小数,积就有几位小数。因为要把小数乘法转化成整数乘法,被乘数扩大了多少倍,乘数不变,积也随着扩大了多少倍。因此必须再把积缩小多少倍。
计算小数乘以整数,先按照整数乘法的计算方法算出积,再看被乘数中有几位小数,就从积的右边起数出几位,点上小数点。
部分小数类型定义
纯小数:整数部分是零的小数如0.1,绝对值一定小于1。
带小数:整数部分是1或1以上的小数如1.1,绝对值一定大于等于1。
一个小数,从小数部分的某一位起,一个数字或几个数字,依次不断地重复出现,这个小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字
叫做这个循环小数的循环节。例如:0.33……循环节是“3”
2.14242……循环节是“42”
纯循环小数:循环节从小数部分第一位开始的。(例如:0.666……)
混循环小数:循环节不是从小数部分第一位开始的。(例如:0.5666……)
简便记法:写循环小数时,为了简便,小数的循环部分只写出
第一个循环节。如果循环节只有一个数字,就在这个数字上加一个圆点,如果循环节有一个以上的数字,就在这个循环节的首位和末位的数字上各加一个圆点。
小数_小数 -性质
小数点的末尾添上0或者去掉0,小数的大小不变。
小数_小数 -分类
纯小数
整数部分是零的小数如0.1,绝对值一定小于1。如:0.12;0.945;0.403等带小数
整数部分是1或1以上的小数如1.1,绝对值一定大于等于1。如:1.2345;9.45;1.43等一个小数,从小数部分的某一位起,一个数字或几个数字,依次不断地重复出现,这个小数叫做循环小数。循环节
一个循环小数的小数部分,依次不断重复出现的数字叫做这个循环小数的循环节。例如:0.33……循环节是“3”2.14242……循环节是“42”纯循环小数:循环节从小数部分第一位开始的。(例如:0.666……)混循环小数:循环节不是从小数部分第一位开始的。(例如:0.5666……)简便记法
写循环小数时,为了简便,小数的循环部分只写出第一个循环节。如果循环节只有一个数字,就在这个数字上加一个圆点,如果循环节有一个以上的数字,就在这个循环节的首位和末位的数字上各加一个圆点。小数_小数 -规则
根据十进制的位值原则,把十进分数仿照整数的写法写成不带分母的形式,这样的数叫做小数.小数中的圆点叫做小数点,它是一个小数的整数部分和小数部分的分界号,小数点左边的部分是整数部分,小数点右边的部分是小数部分.整数部分是零的小数叫做纯小数,整数部分不是零的小数叫做带小数.例如0.3是纯小数,3.1是带小数.
小数_小数 -分类
小数分为纯小数,带小数,有限小数,无限小数
无限小数包括无限循环小数和无限不循环小数
小数_小数 -读法
有两种:一种是按照分数的读法来读.带小数的整数部分按整数读法读;小数部分按分数读法读.例如:0.38读作百分之三十八,14.56读作十四又百分之五十六.另一种读法,整数部分仍按整数的读法来读,小数点读作“点”,小数部分顺次读出每个数位上的数字,若几个零重复,不可只读一个0.例如:0.45读作零点四五;56.032读作五十六点零三二;1.0005读作一点零零零五.小数_小数 -比较
小数大小的比较方法与整数基本相同,即从高位起,依次把相同数位上的数加以比较.因此,比较两个小数的大小,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大;因为小数是十进分数,所以有下列性质:①在小数的末尾添上零或去掉零,小数的大小不变.例如;2.4=2.400,0.060=0.06.②小数点移动会引起小数大小发生变化.把小数点分别向右移动一位、二位、三位…位,则小数的值分别扩大10倍、100倍、1000倍……例如:把7.4扩大10倍是74,扩大100倍是740……如果把小数点分别向左移动一位、二位、三位…则小数的值分别缩小到原来的十分之一、百分之一、千分之一…....例如:把7.4缩小到原来的十分之1是0.74,缩小到原来的百分之一是0.074……
小数_小数 -保留
小数保留小数:按要求在舍去部分最高位进行四舍五入运算。无限不循环小数只能用小数表示不能用分数表示,而所有的有限小数和无限循环小数均能用分数表示,小数分为有限小数和无限小数,有限小数如1/5,无限小数包括无限不循环小数(如0.010010001……)和无限循环小数(如1/3)(有理数(rationalnumber):能精确地表示为两个整数之比的数.如3,-98.11,5.72727272……,7/22都是有理数.整数和通常所说的分数都是有理数.有理数还可以划分为正有理数,0和负有理数.在数的十进制小数表示系统中,有理数就是可表示为有限小数或无限循环小数的数.这一定义在其他进位制下(如二进制)也适用.《中国大百科全书》(数学))因此,不矛盾。小数乘以整数:把小数乘法转化成整数乘法计算。先把小数扩大成整数,按照整数乘法去计算,因数扩大了多少倍,积就要缩小多少倍。积的小数位数与被乘数的小数位数有关,被乘数有几位小数,积就有几位小数。因为要把小数乘法转化成整数乘法,被乘数扩大了多少倍,乘数不变,积也随着扩大了多少倍。因此必须再把积缩小多少倍。计算小数乘以整数,先按照整数乘法的计算方法算出积,再看被乘数中有几位小数,就从积的右边起数出几位,点上小数点。
 爱华网
爱华网