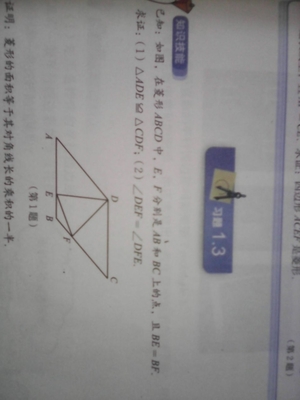
等边三角形(equilateral triangle),又称正三角形,为三边相等的三角形,其三个内角相等,均为60°,它是锐角三角形的一种。有一个内角为60°的等腰三角形是等边三角形。等边三角形也是最稳定的结构。可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),等边三角形的尺规作图再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
等边三角形_等边三角形 -尺规作法
可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),等边三角形的尺规作图再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
等边三角形_等边三角形 -判定方法
(1)三边相等的三角形是等边三角形(定义)。
等边三角形
(2)三个内角都相等的三角形是等边三角形。
(3)有一个内角是60度的等腰三角形是等边三角形。
(4) 两个内角为60度的三角形是等边三角形。
说明:可首先考虑判断三角形是等腰三角形。
提示:【1】三个判定定理的前提不同,判定(1)和(2)是在三角形的条件下,判定(3)是在等腰三角形的条件下。
【2】判定(3)告诉我们,在等腰三角形中,只要有一个角是60度,不论这个角是顶角还是底角,这个三角形就是等边三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
等边三角形_等边三角形 -运用等边三角解题方法
在全等证明题目中往往把等边三角形作为背景图形,在解题时我们要善于运用等边三角形的特殊性来达到证明全等的目的。
等边三角形_等边三角形 -复数性质
等边三角形
A,B,C三点的复数构成正三角形 等价于
等边三角形
其中
;
等边三角形
等边三角形_等边三角形 -相关公式
等边三角形与圆的有关计算公式
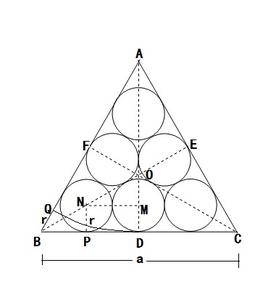
边长关系h=a sin60°=1/2 √3a
r=1/2 a cot(π/3)=1/2 a tan(π/6)=1/6 √3a
R=1/2 a csc(π/3)=1/2 a sec(π/6)=1/3 √3a
S=1/4 na²cot(π/3)=1/4 √3a²
Sr= πr²=1/12πa²;表示内切圆面积,
SR=πR²=1/3πa²;表示外接圆面积。
例:试证等边三角形的高和其边长的比为 √(3/4):1
证明:
作等边三角形的一条高,将等边三角形分为两个全等的直角三角形,
设这个等边三角形的边长为a,则其中一个直角三角形一条直角边长为1/2a,斜边为a(即该等边三角形.由勾股定理,(直角三角形的两直角边的平方和等于斜边的平方),得另一条直角边(即该等边三角形的高)为 √a^2-(1/2a)^2 = √(3/4a) ,即证.
由上,可推导出等边三角形的面积公式:
S=1/2ah= (1/2)×[√(3/4a)]= [(√3)/4]×a^2
等边三角形_等边三角形 -举例证明
有关问题的证明
已知:△ABC中,∠A=60°,且AB+AC=a,
求证:当三角形的周长最短时,三角形是等边三角形。
证明:AC=a-AB
根据余弦定理
BC2=AB2+BC2-2AB*BC*cosA
BC2=AB2+BC2-AB*BC=AB2+(a-AB)2-AB*(a-AB)=3AB2-3a*AB+a2=3(AB-a/2)2+a2/4
所以当AB=a/2时,BC=a/2最小
AC=a-a/2=a/2
这时,周长为AB+AC+BC=a+BC=a+a/2=3a/2最短
AB=AC=BC=a/2
所以当周长最短时的三角形是正三角形。
 爱华网
爱华网