gamma分布_Gamma分布 -Gamma分布的定义
Gamma分布的定义
设α,β是正常数,如果X的密度是:
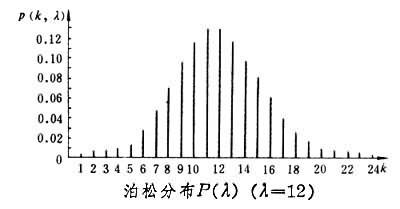
Gamma分布中2参数为形状参数α(shape parameter)和尺度参数β(scale parameter),当α为正整数时,分布可看作α个独立的指数分布之和,当k趋向于较大数值时,分布近似于正态分布。下图为概率密度函数(图中形状参数k为(shape parameter)和尺度参数θ为(scale parameter))。
性质:
1、β=n,Γ(n,α)就是Erlang分布。Erlang分布常用于可靠性理论和排队论中 ,如一个复杂系
统中从第 1 次故障到恰好再出现 n 次故障所需的时间;从某一艘船到达港口直到恰好有 n 只船到达所
需的时间都服从 Erlang分布;
2、当β= 1 时,Γ(1,α) 就是参数为α的指数分布,记为exp (α) ;
3、当α =n/2 ,β=1/2时,Γ (n/2,1/2)就是数理统计中常用的χ2( n) 分布。
4、数学期望(均值)、方差分别为
E( X) =β/α,D ( X) =β/(α*α)
5、(Gamma 分布的可加性):设随机变量 X1 , X2 , …, Xn 相互独立,并且都服从Gamma 分布,即Xi ~Γ(βi , α),i =1 ,2 , …, n , 则:
X1 + X2 + …+ Xn ~ Γ(β1 +β2 + …+βn , α)
gamma分布_Gamma分布 -"Gamma分布" 英文对照
gamma distribution; form of gamma distribution;
gamma分布_Gamma分布 -"Gamma分布" 在学术文献中的解释
1、在地震序列的有序性、地震发生率的齐次性、计数特征具有独立增量和平稳增量情况下,可以导出地震发生i次时间的概率密度为Gamma密度函数(亦称为Gamma分布)
 爱华网
爱华网