错位相减法是一种常用的数列求和方法,应用于等比数列与等差数列相乘的形式。形如An=BnCn,其中Bn为等差数列,Cn为等比数列;分别列出Sn,再把所有式子同时乘以等比数列的公比,即kSn;然后错一位,两式相减即可。如果数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和可用此法来求和。
错位相减_错位相减法 -简介
如果数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和可用此法来求,如等比数列的前n项和公式就是用此法推导的
错位相减_错位相减法 -错位相减法解题
错位相减法是求和的一种解题方法。在题目的类型中:一般是a前面的系数和a的指数是相等的情况下才可以用。
例子1
S=a+2a^2+3a^3+……+(n-2)a^(n-2)+(n-1)a^(n-1)+na^n (1)
在(1)的左右两边同时乘上a。 得到等式(2)如下:
aS= a^2+2a^3+3a^4+……+(n-2)a^(n-1)+(n-1)a^n+na^(n+1) (2)
用(1)-(2),得到等式(3)如下:
(1-a)S=a+(2-1)a^2+(3-2)a^3+……+(n-n+1)a^n-na^(n+1) (3)
(1-a)S=a+a^2+a^3+……+a^(n-1)+a^n-na^(n+1)
S=a+a^2+a^3+……+a^(n-1)+a^n用这个的求和公式。
(1-a)S=a+a^2+a^3+……+a^(n-1)+a^n-na^(n+1)
最后在等式两边同时除以(1-a),就可以得到S的通用公式了。
例子2
求和Sn=1+3x+5x^2+7x^3+……..+(2n-1)・x^(n-1)(x不等于0)
解:当x=1时,Sn=1+3+5+…..+(2n-1)=n^2
当x不等于1时,Sn=1+3x+5x^2+7x^3+……..+(2n-1)・x^(n-1)
所以xSn=x+3x^2+5x^3+7x^4……..+(2n-1)・x^n
所以两式相减的(1-x)Sn=1+2x[1+x+x^2+x^3+...+x^(n-2)]-(2n-1)・x^n
化简得:Sn=(2n-1)・x地n+1次方-(2n+1)・x^n+(1+x)/(1-x)^2
Sn=(2n+1)*2^n
Sn=3*2+5*4+7*8+...+(2n+1)*2^n
2Sn=3*4+5*8+7*16+...+(2n-1)*2^n+(2n+1)*2^(n+1)
两式相减得
-Sn=6+2*4+2*8+2*16+...+2*2^n-(2n+1)*2^(n+1)
=6+2*(4+8+16+...+2^n)-(2n+1)*2^(n+1)
=6+2^(n+2)-8-(2n+1)*2^(n+1) (等比数列求和)
=(1-2n)*2^(n+1)-2
所以Sn=(2n-1)*2^(n+1)+2
例子3
求等比数列求和公式
Sn= 1/2+1/4+1/8+....+1/2^n
两边同时乘以1/2
1/2Sn= 1/4+1/8+....+1/2^n+1/2^(n+1)(注意跟原式的位置的不同,这样写看的更清楚些)
两式相减
1/2Sn=1/2-1/2^(n+1)
Sn=1-1/2^n
例题1
已知等差数列an中,a1=3,点(an,an+1(角码,后不解释))在直线y=x+2上
①求数列an的通项公式
②若bn=an×3的n次方,求数列前n项和Tn
解:①点(an,an+1)在直线y=x+2上,an+1=an+2(2为常数)
即an+1-an=2.所以an是以3为首项,2为公差的等差数列
②bn=an×3^n,bn=(2n+1)×3^n
Tn=3×3+5×3²+7×3³+…+(2n-1)×3的n-1次方+(2n+1)×3^n……一
3Tn=3×3²+5×3³+…+(2n-1)×3的n次方+(2n+1)×3^(n+1)……二
一减二得 9+2×(9(1-3的n-1次方)1-3)-(2n+1)×3的n+1次方=-2n×3^(n+1)
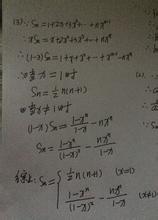
所以Tn=n×3^(n+1)
故得出结果。
 爱华网
爱华网