发布时间:2018年04月10日 21:44:22分享人:人艰不拆来源:互联网30
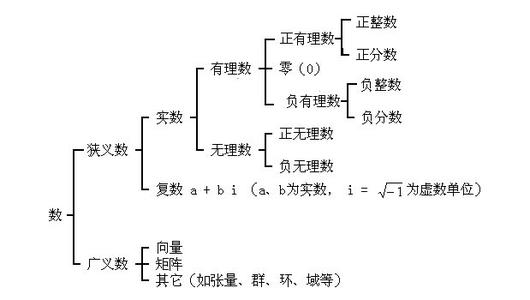
通俗地认为,包含所有有理数和无理数的集合就是实数集。通常用大写字母R表示。18世纪,微积分学在实数的基础上发展起来。但当时的实数集并没有精确的定义。直到1871年,德国数学家康托尔第一次提出了实数的严格定义。
实数集_实数集 -公理
18世纪,微积分学在实数的基础上发展起来。但当时的实数集并没有精确的定义。直到1871年,德国数学家康托尔第一次提出了实数的严格定义。定义是由四组公理为基础的:
1、实数集_实数集 -加法公理
1.1对于任意属于集合R的元素a、b,可以定义它们的加法a+b,且a+b属于R; 1.2加法有恒元0,且a+0=0+a=a(从而存在相反数); 1.3加法有交换律,a+b=b+a; 1.4加法有结合律,(a+b)+c=a+(b+c)。 2、实数集_实数集 -乘法公理
: 2.1对于任意属于集合R的元素a、b,可以定义它们的乘法a・b,且a・b属于R; 2.2乘法有恒元1,且a・1=1・a=a(从而除0外存在倒数); 2.3乘法有交换律,a・b=b・a; 2.4乘法有结合律,(a・b)・c=a・(b・c); 2.5乘法对加法有分配率,即a・(b+c)=(b+c)・a=a・b+a・c。 3、
实数集_实数集 -序公理
: 3.1任何x、y属于R,xy中有且只有一个成立; 3.2若x0,则x・z
实数集_实数集 -完备公理
实数集_实数集 -总结
符合以上四组公理的任何一个集合都叫做实数集,实数集的元素称为实数。
爱华网本文地址 » http://www.aihuau.com/a/8104020103/156280.html
更多阅读
本文简要地介绍ZFC集合论中各公理的意义及作用。首先,ZFC集合论中的公理大致分为3组:1、外延公理。2、子集公理模式、无序对公理、并集公理、幂集公理、无穷公理、替换公理模式。3、正则公理(或 基础公理)、选择公理(记作 AC)。下面

特别说明:完整45期数字信号处理教程,原创高性能示波器代码全开源地址:链接第32章实数FFT的实现本章主要讲解实数的浮点和定点Q31,Q15的实现。关于这部分的知识点和函数的计算结果上,官方的文档有一些小错误,在章节中会跟大家详细讲述,还有

空间为实数多维度,时间为虚数多维度,时间是虚数空间,空间是虚数虚数时间在我们经验中空间维度是实实在在的,我们可以在三维空间中上下左右自由移动空间是多维度的,但是每个空间维度都是实实在在的实数;在我们经验中,时间是虚无飘渺,看不见

相信学过数学分析的朋友都有这样的经验,讲到实数系基本定理的时候,只看到若干定理相互推导,好像谁都可以来充当公理,结果就被搞得一头雾水,根本不知道它想要干什么。其实,实数系并不是讨论这些问题的理想舞台,这些内容得到点集拓扑与泛函分

实数R代表RealNumber(实数),复数的C代表Complex Number(复数),自然数N代表NaturalNumber(自然数);而有理数集的Q是英语/德语Quotient(商)的首字母,整数和分数统称为有理数,任何一个有理数都可以写成分数m/n(m,n都是整数,且n≠0)的形式,由于两个数相

 爱华网
爱华网



