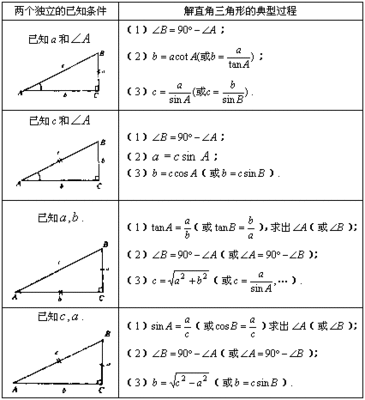
在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
三角形三边关系_三角形三边关系 -一般
设三角形三边为a,b,c则
a+b>c,a>c-b
b+c>a,b>a-c
a+c>b,c>b-a
三角形三边关系
如图,
任意△ABC,求证AB+AC>BC。
证明:在BA的延长线上取AD=AC
则∠D=∠ACD(等边对等角)
∵∠BCD>∠ACD
∴∠BCD>∠D
∴BD>BC(大角对大边)
∵BD=AB+AD=AB+AC
∴AB+AC>BC
三角形三边关系_三角形三边关系 -基本定理
在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
设三角形三边为a,b,c则
a+b>c
a+c>b
b+c>a
a-b
a-c
b-c
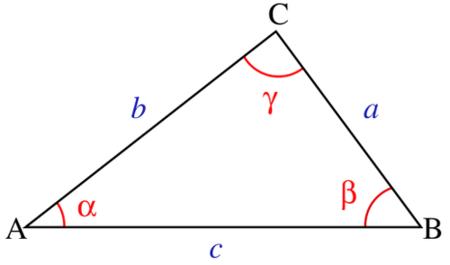
在直角三角形中,设a、b为直角边,c为斜边。
则两直角边的平方和等于斜边平方。(勾股定理)
在等边三角形中,a=b=c
在等腰三角形中,若a,b为两腰,则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下,c^2=a^2+b^2-2abcosc
三角形三边关系_三角形三边关系 -特殊
直角三角形
性质1:直角三角形两直角边的平方和等于斜边的平方。 性质2:在直角三角形中,两个锐角互余。 性质3:在直角三角形中,斜边上的中线等于斜边的一半。
性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。性质5:如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1) AD^2=BD・DC,
(2) AB^2=BD・BC , 射影定理图
(3) AC^2=CD・BC 。 等积式 (4)ABXAC=ADXBC (可用面积来证明) (5)直角三角形的外接圆的半径R=1/2BC,
(6)直角三角形的内切圆的半径r=1/2(AB+AC-BC)(公式一);r=AB*AC/(AB+BC+CA)(公式二)
三角形三边关系
等腰直角三角形三边之比:1:1:根号二
 爱华网
爱华网