一个正整数的阶乘(英语:factorial)是所有小于及等于该数的正整数的积,并且有0的阶乘为1。自然数n的阶乘写作n!。1808年,基斯顿・卡曼引进这个表示法。亦即n!=1×2×3×...×n。阶乘亦可以递归方式定义:0!=1,n!=(n-1)!×n。阶乘亦可定义于整个实数(负整数除外),其与伽玛函数的关系为:n!可质因子分解为,如6!=24×32×51。
阶乘符号_阶乘符号 -阶乘符号
1751年,欧拉以大写字母M表示m阶乘,即 M=1×2×3×…×m
1799年,鲁非尼在他出版的方程论着述中,则以小写字母π表示m阶乘,而在1813年,高斯则以Π(n)来表示n阶乘。而用来表示n阶乘的方法起源于英国,但仍未能确定始创人是谁。直至1827年,由于雅莱特的建议而得到流行,现在有时也会 以这个符号作为阶乘符号。
而最先提出阶乘符号n!的人是克拉姆 (1808),后来经过欧姆等人的提倡而流行,直至现在仍然通用。
当n较大时,直接计算n!变得不可能,这时可通过斯特灵(Stirling)公式计算近似算或取得大小范围。
阶乘符号_阶乘符号 -阶乘数
由fxccommercial提出,系fxccommercial本人发现并归纳整理成为一个新的数学定理猜想.这个公式描述的是,从大到小排列的n+1个数,对每个数取n次方,用(-1)^nC_n^k做系数,实现奇偶项数的差项和,则这列数的和为n!,目前fxccommercial已得到一个关于他的推论,经验证是正确的。历史上并没有人得到过类似的公式,可以认为它是人类对数学的又一个深刻的认识,但目前关于这个定理的证明尚无人能给出,笔者期待这个定理证明的解决.
约定∑_k=0_n 表示对从0到n的n+1项求和,则该定理表述为: ∑_k=0_n (-1)^k*C_n^k*(a-mk)^n = m^n*n! (a属于R, k,m,n属于N) n^k : n 的 k 次方, ^ 用来表示上标; a/b: a 除以 b; a*b: a 乘以 b,有时可以忽略*; n!: n 的阶乘; [x]: 不超过x的最大整数; : x的小数部分; a_n: 数列第n项, _ 用来表示下标n; C_n^k: 组合数,表示n个元素里取k个元素.
阶乘符号_阶乘符号 -pascal阶乘数与全排列
所谓阶乘数是指其最低位的基为1,即逢一进一,每高一位则基加一,即进位依次为二、三…,n位阶乘数共有n!个。如三位阶乘数从小到大依次为:000,010,100,110,200,210。设n元集合S={a 0 , a1 , a2, … an-1},则S的全排列与n位阶乘数一一对应。对应方式为:从n个元素中选取第一个元素有n种方法,被选取的元素的下标值为0到n-1之间的一个整数,将这个数作为n位阶乘数的最高位,将剩下的元素按下标从0到n-2重新编号,重新编号时不改变它们的相对次序,则选取第二个元素有n-1种方法,被选取的元素的下标值为0到n-2之间的一个整数,将这个数作为n位阶乘数的次高位,…,选取最后一个元素只有1种方法,被选取的元素的下标值为0,将这个数作为n位阶乘数的最低位,这样任何一种排列必可对应一个n位阶乘数,显然这种对应关系是一一对应的。问题:请用阶乘数法生成1到n的全排列。 [算法设计] 首先用最低位加一的方法依次产生所有的n位阶乘数,对任意一个 n位阶乘数用上述方法求出其对应的排列。 [参考程序] program ex5(input,output); const maxn=9; type arraytype=array[0..maxn] of integer; var i,j,n:integer; a,b,p:arraytype; begin write('Input n:'); readln(n); for i:=0 to n-1 do b[i]:=0; while b[n]=0 do begin for i:=0 to n-1 do a[i]:=i+1; for i:=n-1 downto 0 do begin p[i]:=a[b[i]]; for j:=b[i] to i-1 do a[j]:=a[j+1] end; for i:=n-1 downto 0 do write(p[i],' '); write(' ':20-2*n); b:=b+1; i:=0; while b[i]>i do begin b[i]:=0; b[i+1]:=b[i+1]+1; i:=i+1 end end; writeln end. 解释程序
阶乘符号_阶乘符号 -计算
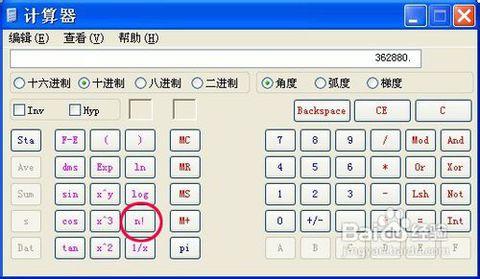
计算n!时,当n不太大时,普通的 科学计算机都可以计算,能够处理不超过数值的计算机可以计算至69!。
当n很大时,可以用 斯特林公式估计
 爱华网
爱华网